Question

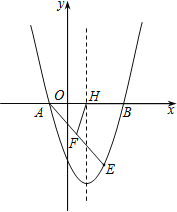
【题目】如图，抛物线y=x2+bx+c经过点A（﹣1，0），B（3，0）．请解答下列问题：

（1）求抛物线的解析式；

（2）点E（2，m）在抛物线上，抛物线的对称轴与x轴交于点H，点F是AE中点，连接FH，求线段FH的长．

注：抛物线y=ax2+bx+c（a≠0）的对称轴是x=．

Answer 1

【答案】（1）；（2）．

【解析】

（1）把A,B两点坐标代入，求待定系数b,c，进而确定抛物线的解析式；（2）连接BE，点F是AE中点，H是AB中点，则FH为三角形ABE的中位线，求出BE的长，FH就知道了，先由抛物线解析式求出点E坐标，根据勾股定理可求BE，再根据三角形中位线定理求线段HF的长．

解：（1）∵抛物线y=x2+bx+c经过点A（﹣1，0），B（3，0），∴把A,B两点坐标代入得：，解得：，

∴抛物线的解析式是：；

（2）∵点E（2，m）在抛物线上，

∴把E点坐标代入抛物线解析式y=-2x-3得：m=4﹣4﹣3=﹣3，

∴E（2，﹣3），

∴BE==．

∵点F是AE中点，点H是抛物线的对称轴与x轴交点，即H为AB的中点，

∴FH是三角形ABE的中位线，

∴FH=BE=×=．

∴线段FH的长．