题目内容
【题目】如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.
(1)求sin∠CAH的值;
(2)如果CD=![]() ,求BE的值.
,求BE的值.
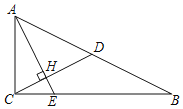
【答案】(1)![]() ;(2)3
;(2)3
【解析】
(1)由勾股定理得出AC=![]() =
=![]() CH,由锐角三角函数定义即可得出答案;
CH,由锐角三角函数定义即可得出答案;
(2)根据sinB的值,可得出AC:AB=1:![]() ,由AB=2
,由AB=2 ![]() ,得AC=2,设CE=x(x>0),则AE=
,得AC=2,设CE=x(x>0),则AE=![]() x,由勾股定理得出方程,求出CE=1,从而得出BE.
x,由勾股定理得出方程,求出CE=1,从而得出BE.
解:(1)∵AE⊥CD,
∴∠AHC=90°,
∵AH=2CH,
∴由勾股定理得:AC=![]() =
=![]() CH,
CH,
∴sin∠CAH=![]() ;
;
(2)∵∠ACB=90°,CD是斜边AB上的中线,
∴AB=2CD=2 ![]() ,
,
∴∠B=∠BCD,
∵AE⊥CD,
∴∠CAH+∠ACH=90°,
又∵∠ACB=90°,
∴∠BCD+∠ACH=90°,
∴∠B=∠BCD=∠CAH,
∵sinB=![]() =sin∠CAH=
=sin∠CAH=![]() =
=![]() ,
,
∴AC:AB=1:![]() ,
,
∴AC=2.
设CE=x(x>0),则AE=![]() x,
x,
在Rt△ACE中,由勾股定理得:x2+22=(![]() x)2,
x)2,
解得:x=1,
∴CE=1,
在Rt△ABC中,由勾股定理得:BC=![]() =
=![]() =4,
=4,
∴BE=BC﹣CE=3.

练习册系列答案
相关题目
【题目】已知抛物线![]() 上部分点的横坐标x与纵坐标y的对应值如下表
上部分点的横坐标x与纵坐标y的对应值如下表
x | … | -2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | -4 | 0 | 2 | 2 | 0 | -4 | … |
下列结论:①抛物线开口向下;②当![]() 时,y随x的增大而减小;③抛物线的对称轴是直线
时,y随x的增大而减小;③抛物线的对称轴是直线![]() ;④函数
;④函数![]() 的最大值为2.其中所有正确的结论为( )
的最大值为2.其中所有正确的结论为( )
A.①②③B.①③C.①③④D.①②③④