Question

【题目】已知AB为⊙O的直径.

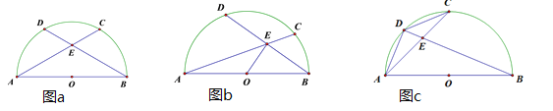
（1）如图a，点D为 的中点，当弦BD=AC时，求∠A.

（2）如图b，点D为的中点，当AB=6，点E为BD的中点时，求OE的长.

（3）如图c，点D为上任意一点（不与A、C重合），若点C为的中点，探求BD、AD、CD之间的数量关系，直接写出你探求的结论，不要求证明.

Answer 1

【答案】（1）30°；（2）；（3）BD－AD=CD

【解析】

（1）连接OC，由BD=AC证明，进一步证明C为的中点，从而可证∠A=∠COB=××180°=30°；

（2）连结OD，BC，证明△DEF≌△BEC，分别OD，OF，BC，DF，AC以及EF的长，

在Rt△OFE中运用勾股定理即可求得OE=；

（3）连接BC，可证明∠BAC=∠BDC=45°，过点C作CF⊥CD交BD于点F，证明△ACD≌△BCF，根据BD=BF+DF可得结论.

(1) 连结OC

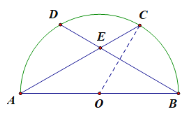
∵点D为的中点，

∴

∵BD=AC

∴

∴，即点C为的中点.

∴

∴∠A=∠COB=××180°=30°.

(2）连结OD，BC.

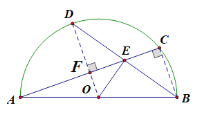
∵AB为⊙O的直径,

∴∠C=90ｏ

∵点D为的中点，半径OD所在的直线为⊙O的对称轴

∴点A的对应点为C

∴OD⊥AC，OD分AC,即：AF=CF，

∵点E为BD的中点，

∴BE=DE，

在△DEF和△BEC中

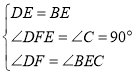
∴△DEF≌△BEC

∴CE=EF, BC=DF

∵AO=BO, AF=CF

∴OF=BC=DF ，

又AB=6，

∴OD=3

∴OF=1, BC=DF=2

在Rt△ABC中，AB=6，BC=2,由勾股定理求得AC=4，

∵点F为AC的中点，点E为FC的中点

∴EF=，

在Rt△OFE中，EF=，OF=1,由勾股定理求得OE=

（3）BD、AD、CD之间的关系为：BD－AD=CD

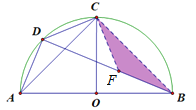
连接BC，

∵AB是直径，点C为的中点，

∴∠ACB=90°,AC=BC，

∴∠BAC=∠BDC=45°，

过点C作CF⊥CD交BD于点F，

∴△DCF是等腰直角三角形，

∴CD=CF，DF=CD，

∵∠ACD=∠BCF=90°-∠ACF，

又AC=BC，CD=CF

∴△ACD≌△BCF

∴AD=BF

∵BD=BF+DF

∴BD=AD+CD，即BD－AD=CD.