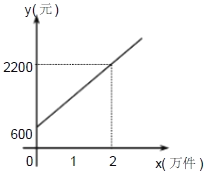
题目内容
【题目】欧几里得是古希腊著名数学家、欧氏几何学开创者.下面问题是欧几里得勾股定理证法的一片段,同学们,让我们一起来走进欧几里得的数学王国吧!
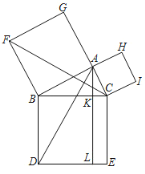
已知:在Rt△ABC,∠A=90°,分别以AB、AC、BC为边向外作正方形,如图,连接AD、CF,过点A作AL⊥DE分别交BC、DE于点K、L.
(1)求证:△ABD≌△FBC
(2)求证:正方形ABFG的面积等于长方形BDLK的面积,即:![]()
【答案】(1)见解析;(2)见解析
【解析】
(1)根据正方形的性质可得AB=FB,BD=BC,∠FBA=∠CBD=90°,从而证出∠FBC=∠ABD,然后利用SAS即可证出结论;
(2)根据平行线之间的距离处处相等可得![]() ,然后根据全等三角形的性质可得
,然后根据全等三角形的性质可得![]() ,从而证出结论.
,从而证出结论.
(1)证明:∵四边形ABFG、四边形BDEC是正方形
∴AB=FB,BD=BC,∠FBA=∠CBD=90°
∴∠FBA+∠ABC=∠CBD+∠ABC
即∠FBC=∠ABD
在△ABD和△FBC中

∴△ABD≌△FBC(SAS)
(2) ∵ GC∥FB,AL∥BD
∴![]() ,
,
∵△ABD≌△FBC
∴![]()
∴![]()

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目