Question

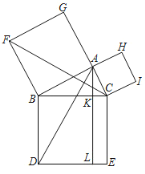
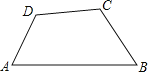
【题目】如图，在四边形中，，则（ ）

A.B.C.D.

Answer 1

【答案】D

【解析】

连接AC，作CF⊥AB于F，CE⊥AD交AD的延长线于E．证明△CED≌△CFB，Rt△ACE≌Rt△ACF，利用全等三角形的性质解决问题即可．

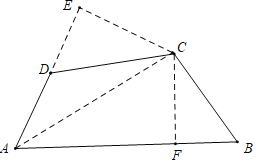
解：如图，连接AC，作CF⊥AB于F，CE⊥AD交AD的延长线于E．

∵∠B=60°，∠ADC=120°，
∴∠DAB+∠DCB=180°，
∵∠E+∠CFA=180°，
∴∠EAF+∠ECF=180°，
∴∠ECF=∠DCB，
∴∠DCE=∠BCF，
∵∠E=∠CFB=90°，CD=CB，

在△CED和△CFB中，

，
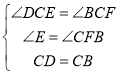∴△CED≌△CFB（AAS），
∴CE=CF，DE=BF=BCcos60°=a，
∵AC=AC，CE=CF，

在Rt△ACE和Rt△ACF中，

，
∴Rt△ACE≌Rt△ACF（HL），
∴AE=AF，
∴AB-AD=AF+BF-（AE-DE）=2DE=a，
故选：D．