题目内容
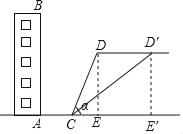
【题目】如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

【答案】学校至少要把坡顶D向后水平移动7米才能保证教学楼的安全.
【解析】试题分析:假设点D移到D′的位置时,恰好∠α=39°,过点D作DE⊥AC于点E,作D′E′⊥AC于点E′,根据锐角三角函数的定义求出DE、CE、CE′的长,进而可得出结论.
试题解析:假设点D移到D′的位置时,恰好∠α=39°,过点D作DE⊥AC于点E,作D′E′⊥AC于点E′,
∵CD=12米,∠DCE=60°,
∴DE=CDsin60°=12×![]() =6
=6![]() 米,CE=CDcos60°=12×
米,CE=CDcos60°=12×![]() =6米.
=6米.
∵DE⊥AC,D′E′⊥AC,DD′∥CE′,
∴四边形DEE′D′是矩形,
∴DE=D′E′=6![]() 米.
米.
∵∠D′CE′=39°,
∴CE′=![]() ≈
≈![]() ≈12.8,
≈12.8,
∴EE′=CE′﹣CE=12.8﹣6=6.8≈7(米).
答:学校至少要把坡顶D向后水平移动7米才能保证教学楼的安全.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
男、女生所选项目人数统计表
项目 | 男生(人数) | 女生(人数) |
机器人 | 7 | 9 |
3D打印 | m | 4 |
航模 | 2 | 2 |
其他 | 5 | n |
根据以上信息解决下列问题:
(1)m=_____,n=_____;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为_____°;
(3)从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.