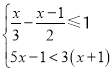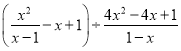ЬтФПФкШн
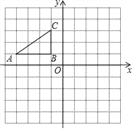
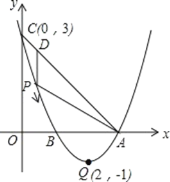
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯп y=ax2+bx+cЃЈaЁй0ЃЉЕФЖЅЕузјБъЮЊ QЃЈ2ЃЌЉ1ЃЉЃЌЧвгы y жсНЛгкЕу CЃЈ0ЃЌ3ЃЉЃЌ гы x жсНЛгк AЁЂB СНЕуЃЈЕу A дкЕу B ЕФгвВрЃЉЃЌЕу P ЪЧХзЮяЯпЩЯЕФвЛЖЏЕуЃЌДгЕу C биХзЮяЯпЯђ Еу A дЫЖЏЃЈЕу P гы A ВЛжиКЯЃЉЃЌЙ§Еу P зї PDЁЮy жсЃЌНЛ AC гкЕу DЃЎ
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФКЏЪ§ЙиЯЕЪНМА AЁЂB СНЕуЕФзјБъЃЛ
ЃЈ2ЃЉЧѓЕу P дкдЫЖЏЕФЙ§ГЬжаЃЌЯпЖЮ PD ЕФзюДѓжЕЃЛ
ЃЈ3ЃЉШєЕу P гыЕу Q жиКЯЃЌЕу E дк x жсЩЯЃЌЕу F дкХзЮяЯпЩЯЃЌЮЪЪЧЗёДцдквд AЃЌPЃЌEЃЌF ЮЊЖЅ ЕуЕФЦНааЫФБпаЮЃПШєДцдкЃЌжБНгаДГіЕу F ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
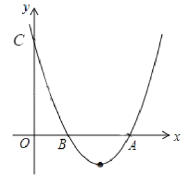
ЁОД№АИЁП(1)y = x - 4x + 3ЃЌA (3ЃЌ0)ЃЌB (1ЃЌ0) ЃЛЃЈ2ЃЉ ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() (
(![]() ЃЌ1) ЃЌ
ЃЌ1) ЃЌ![]() (
(![]() ЃЌ1) ЃЎ
ЃЌ1) ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉвбжЊХзЮяЯпЕФЖЅЕузјБъЃЌПЩНЋХзЮяЯпЕФНтЮіЪНЩшЮЊЖЅЕуЪНЃЌШЛКѓНЋКЏЪ§ЭМЯѓОЙ§ЕФCЕузјБъДњШыЩЯЪНжаЃЌМДПЩЧѓГіХзЮяЯпЕФНтЮіЪНЃЌСюy=0ЃЌЧѓГіСНИљЃЌМДПЩЕУГіAЁЂBЕФзјБъЃЛ
ЃЈ2ЃЉгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпACЕФНтЮіЪНЃЌЩшDЃЈxЃЌЉx+3ЃЉЃЌдђPЃЈxЃЌxЉ4x+3ЃЉЃЌБэЪОГіPDЕФГЄЃЌРћгУЖўДЮКЏЪ§ЕФаджЪМДПЩНтД№ЃЛ
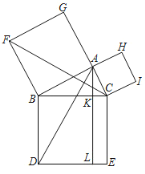
ЃЈ3ЃЉЕБЕу P ЕФзјБъЮЊ PЃЈ2ЃЌЉ1ЃЉЃЈМДЖЅЕу QЃЉЪБЃЌЗжСНжжЧщПіЬжТлЃКЂйвд AP ЮЊБпНјааЙЙдьЦНааЫФБпаЮЃЛЂквд AP ЮЊЖдНЧЯпНјааЙЙдьЦНааЫФБпаЮЃЎ
ЃЈ1ЃЉЁпХзЮяЯпЕФЖЅЕуЮЊQЃЈ2ЃЌЉ1ЃЉЃЌЁрЩшХзЮяЯпЕФНтЮіЪНЮЊy=aЃЈxЉ2ЃЉ2Љ1ЃЌНЋCЃЈ0ЃЌ3ЃЉДњШыЩЯЪНЃЌЕУЃКЁЁ3=aЃЈ0Љ2ЃЉ2Љ1ЃЌНтЕУЃКa=1ЃЌЁрy=ЃЈxЉ2ЃЉ2Љ1ЃЌМДy=x2Љ4x+3ЃЎ
Сюy=0ЃЌЕУЃКx2Љ4x+3=0ЃЌНтЕУЃКx1=1ЃЌx2=3ЃЎ
ЁпЕуAдкЕуBЕФгвБпЃЌЁрAЃЈ3ЃЌ0ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЛ
ЃЈ2ЃЉЩшжБЯп AC ЕФКЏЪ§ЙиЯЕЪНЮЊ y=mx+nЃЌНЋ AЃЈ3ЃЌ0ЃЉЃЌCЃЈ0ЃЌ3ЃЉДњШыЩЯЪНЕУЃК![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌЁрy=Љx+3ЃЎ
ЃЌЁрy=Љx+3ЃЎ
ЁпD дк y=Љx+3 ЩЯЃЌP дк y=x2Љ4x+3 ЩЯЃЌЧв PDЁЮy жсЃЌЁрЩшDЃЈxЃЌЉx+3ЃЉЃЌдђPЃЈxЃЌxЉ4x+3ЃЉЃЌЁрPD=Љx+3ЃЃЈx2Љ4x+3ЃЉ= Ѓx2+3x=![]() ЃЌЁрЕБ x =
ЃЌЁрЕБ x = ![]() ЪБЃЌPD ШЁЕУзюДѓжЕЮЊ
ЪБЃЌPD ШЁЕУзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЕБЕу P ЕФзјБъЮЊ PЃЈ2ЃЌЉ1ЃЉЃЈМДЖЅЕу QЃЉЪБЃК
Ђйвд AP ЮЊБпНјааЙЙдьЦНааЫФБпаЮЃЎЦНвЦжБЯп AP НЛ x жсгкЕу EЃЌНЛХзЮяЯпгк FЃЎ
ЁпPЃЈ2ЃЌЉ1ЃЉЃЌЁрПЩЩш FЃЈxЃЌ1ЃЉЃЌЁрxЉ4x+3=1ЃЌ![]() =
=![]() ЃЌ
ЃЌ![]() =
=![]() ЃЌЁрЗћКЯЬѕМўЕФ F ЕугаСНИіЃЌМД F1ЃЈ
ЃЌЁрЗћКЯЬѕМўЕФ F ЕугаСНИіЃЌМД F1ЃЈ![]() ЃЌ1ЃЉЃЌF2ЃЈ
ЃЌ1ЃЉЃЌF2ЃЈ![]() ЃЌ1ЃЉЃЎ
ЃЌ1ЃЉЃЎ
Ђквд AP ЮЊЖдНЧЯпНјааЙЙдьЦНааЫФБпаЮЃЌВЛДцдкетжжЧщПіЃЌЩсШЅЃЎ
злЩЯЫљЪіЃКЗћКЯЬѕМўЕФ F ЕугаСНИіЃЌМД ![]() ЃЈ
ЃЈ![]() ЃЌ1ЃЉЃЌ
ЃЌ1ЃЉЃЌ![]() ЃЈ
ЃЈ![]() ЃЌ1ЃЉЃЎ
ЃЌ1ЃЉЃЎ

 жЧФмбЕСЗСЗВтПМЯЕСаД№АИ
жЧФмбЕСЗСЗВтПМЯЕСаД№АИ