题目内容
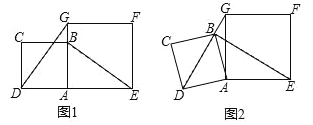
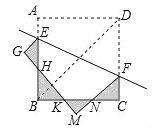
【题目】如图,正方形ABCD的对角线长为![]() .点E、F分别在正方形ABCD的边AB、CD上,四边形EFMG的边MG分别与正方形ABCD的边AB、BC交于点H、K,边MF与正方形ABCD的边BC交于点N.若四边形EFDA沿直线EF折叠后能与四边形EFMG重合,则图中四个三角形△EGH、△HBK、△KMN、△NCF的周长的和为_____.
.点E、F分别在正方形ABCD的边AB、CD上,四边形EFMG的边MG分别与正方形ABCD的边AB、BC交于点H、K,边MF与正方形ABCD的边BC交于点N.若四边形EFDA沿直线EF折叠后能与四边形EFMG重合,则图中四个三角形△EGH、△HBK、△KMN、△NCF的周长的和为_____.
【答案】8
【解析】
由题意可求AB=BC=CD=AD=2,由折叠的性质可得GM=AD,AE=GE,DF=FM,即可证△EGH、△HBK、△KMN、△NCF的周长的和=AB+BC+CD+AD=8.
∵四边形ABCD是正方形,
∴AB=AD=CD=BC,
∵正方形ABCD的对角线长为2![]() ,
,
∴BC2+CD2=8,
∴BC=CD=2=AD=AB,
∵折叠,
∴GM=AD,AE=GE,DF=FM,
∵△EGH、△HBK、△KMN、△NCF的周长的和=GE+EH+GH+BH+HK+BK+KN+KM+MN+NC+FC+FN
∴△EGH、△HBK、△KMN、△NCF的周长的和=AB+BC+CD+AD=8
故答案是:8

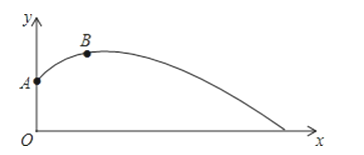
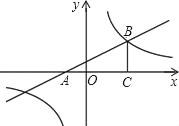
【题目】小明为了检测自己实心球的训练情况,再一次投掷的测试中,实心球经过的抛物线如图所示,其中出手点A的坐标为(0,![]() ),球在最高点B的坐标为(3,
),球在最高点B的坐标为(3,![]() ).
).
(1)求抛物线的解析式;
(2)已知某市男子实心球的得分标准如表:
得分 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
掷远(米) | 8.6 | 8.3 | 8 | 7.7 | 7.3 | 6.9 | 6.5 | 6.1 | 5.8 | 5.5 | 5.2 | 4.8 | 4.4 | 4.0 | 3.5 | 3.0 |
假设小明是春谷中学九年级的男生,求小明在实心球训练中的得分;
(3)在小明练习实心球的正前方距离投掷点7米处有一个身高1.2米的小朋友在玩耍,问该小朋友是否有危险(如果实心球在小孩头顶上方飞出为安全,否则视为危险),请说明理由.