Question

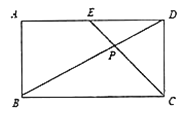
【题目】矩形ABCD中，AB=6，BC=8.点P在矩形ABCD的内部，点E在边BC上，满足△PBE∽△DBC，若△APD是等腰三角形，则PE的长为数___________.

Answer 1

【答案】3或1.2

【解析】由△PBE∽△DBC，可得∠PBE=∠DBC，继而可确定点P在BD上，然后再根据△APD是等腰三角形，分DP=DA、AP=DP两种情况进行讨论即可得.

∵四边形ABCD是矩形，∴∠BAD=∠C=90°，CD=AB=6，∴BD=10，

∵△PBE∽△DBC，

∴∠PBE=∠DBC，∴点P在BD上，

如图1，当DP=DA=8时，BP=2，

∵△PBE∽△DBC，

∴PE：CD=PB：DB=2：10，

∴PE：6=2：10，

∴PE=1.2；

如图2，当AP=DP时，此时P为BD中点，

∵△PBE∽△DBC，

∴PE：CD=PB：DB=1：2，

∴PE：6=1：2，

∴PE=3；

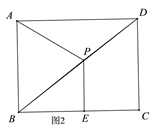
综上，PE的长为1.2或3，

故答案为：1.2或3.