Question

【题目】如图，四边形OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=5，OC=4．

（1）如图①，在AB上取一点D，将纸片沿OD翻折，使点A落在BC边上的点E处，求D、E两点的坐标；

（2）如图②，若OE上有一动点P（不与O，E重合），从点O出发，以每秒1个单位的速度沿OE方向向点E匀速运动，设运动时间为t秒（0＜t＜5），过点P作PM⊥OE交OD于点M，连接ME，求当t为何值时，以点P、M、E为顶点的三角形与△ODA相似？

Answer 1

【答案】（1）点D的坐标为（5，2.5）；（2）当t=2.5或4时，以点P、M、E为顶点的三角形与△ODA相似．

【解析】

（1）由翻折的性质可知OE＝5，然后利用勾股定理可求得CE＝3，从而求得点E的坐标，然后在三角形EDB中，利用翻折的性质和勾股定理可求得AD的长，从而可求得点D的坐标；

（2）首先证明∠EPM＝90°，首先根据相似三角形的性质可知∠PEM＝∠DOA或∠PME＝∠DOA，然后利用相似三角形的性质可求得t的值．

（1）由翻折的性质可知：OE=OA=5，

在Rt△OCE中，CE==3，

∴点E的坐标为（3，4），

∴EB=CB﹣CE=5﹣3=2，

设AD=x，则BD=4﹣x，

由翻折的性质可知：ED=AD=x，

在Rt△BED中，EB2+BD2=ED2，即22+（4﹣x）2=x2，

解得：x=2.5，

∴AD=2.5，

∴点D的坐标为（5，2.5）；

（2）由翻折的性质可知：∠OED=∠DAO=90°，∠DOE=∠DOA，

∵PM∥ED，

∴∠MPE+∠PED=180°，

∴∠MPE=90°，

∴∠MPE=∠DAO，

当点P、M、E为顶点的三角形与△ODA相似时，有△PEM∽△AOD或△PME∽△AOD，

∴∠PEM=∠DOA或∠PME=∠DOA，

①当∠PEM=∠DOA时，在△OPM和△EPM中，，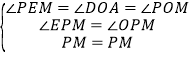

∴△OPM≌△EPM，

∴PE=PO．

∴t=2.5；

②当∠PME=∠DOA时，OP=t，则PE=5﹣t．

∵∠DOE=∠DOA，

∴tan∠DOE=tan∠DOA，

∴，

∴PM=，

∵∠PME=∠DOA，

∴tan∠PME=tan∠DOA，

∴，即，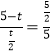

解得：t=4，

综上所述，当t=2.5或4时，以点P、M、E为顶点的三角形与△ODA相似．