题目内容
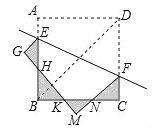
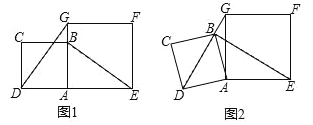
【题目】正方形ABCD和正方形AEFG的边长分别为2和![]() ,点B在边AG上,点D在线段EA的延长线上,连接BE.
,点B在边AG上,点D在线段EA的延长线上,连接BE.
(1)如图1,求证:DG⊥BE;
(2)如图2,将正方形ABCD绕点A按逆时针方向旋转,当点B恰好落在线段DG上时,求线段BE的长.
【答案】(1)答案见解析;(2)![]() .
.
【解析】
(1)由题意可证△ADG≌△ABE,可得∠AGD=∠AEB,由∠ADG+∠AGD=90°,可得∠ADG+∠AEB=90°,即DG⊥BE;
(2)过点A作AM⊥BD,垂足为M,根据勾股定理可求MG的长度,即可求DG的长度,由题意可证△DAG≌△BAE,可得BE=DG.
(1)如图,延长EB交GD于H
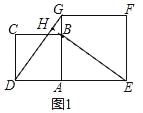
∵四边形ABCD和四边形AEFG是正方形
∴AD=AB,AG=AE,∠DAG=∠BAE=90°
∴△ADG≌△ABE(SAS)
∴∠AGD=∠AEB
∵∠ADG+∠AGD=90°
∴∠ADG+∠AEB=90°
∴DG⊥BE
(2)如图,过点A作AM⊥BD,垂足为M
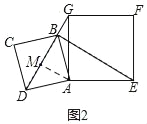
∵正方形ABCD和正方形AEFG的边长分别为2和2![]() ,
,
∴AM=DM=![]() ,∠DAB=∠GAE=90°
,∠DAB=∠GAE=90°
∴MG=![]() =
=![]() ,∠DAG=∠BAE
,∠DAG=∠BAE
∴DG=DM+MG=![]() +
+![]() ,由旋转可得:AD=AB,AG=AE,且∠DAG=∠BAE
,由旋转可得:AD=AB,AG=AE,且∠DAG=∠BAE
∴△DAG≌△BAE(SAS)
∴BE=DG=![]()

练习册系列答案
相关题目