题目内容
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,CE平分∠ACB交⊙O于点E,∠E=30°,交AB于点D,连接AE,则SADC:S△ADE的比值为( ) 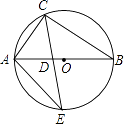
A.![]()
B.![]()
C.![]()
D.1
【答案】C
【解析】解:过C作CF⊥AB于F,连接OE,设AC=a, ∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠B=∠E=30°,
∴∠A=60°,∠ACF=30°,CF= ![]() a,AB=2AC=2a,
a,AB=2AC=2a,
∵CE平分∠ACB交⊙O于E,
∴ ![]() =
= ![]() ,
,
∴OE⊥AB,
∴OE= ![]() AB=a
AB=a
∴S△ADC:S△ADE= ![]() ADCF:
ADCF: ![]() ADOE=
ADOE= ![]() :2.
:2.
故选C.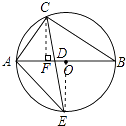
过C作CF⊥AB于F,连接OE,设AC=a,求出CF,OE,根据S△ADC:S△ADE= ![]() ADCF:
ADCF: ![]() ADOE计算即可.
ADOE计算即可.

练习册系列答案
相关题目
【题目】有甲、乙、丙三种糖果混合而成的什锦糖100千克,其中各种糖果的单价和千克数如表所示,商家用加权平均数来确定什锦糖的单价.
甲种糖果 | 乙种糖果 | 丙种糖果 | |
单价(元/千克) | 15 | 25 | 30 |
千克数 | 40 | 40 | 20 |
(1)求该什锦糖的单价.
(2)为了使什锦糖的单价每千克至少降低2元,商家计划在什锦糖中加入甲、丙两种糖果共100千克,问其中最多可加入丙种糖果多少千克?