题目内容
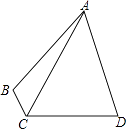
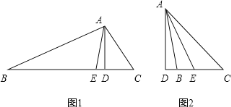
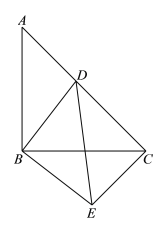
【题目】如图,△ABC和△DBE都是等腰直角三角形,点D在AC上,其中∠ABC=∠DBE=90°.
(1)求∠DCE的度数;
(2)当AB=5,AD:DC=2:3时,求DE的大小;
(3)当点D在线段AC上运动时(D不与A重合),请写出一个反映DA2,DC2,DB2之间关系的等式,并加以证明.
【答案】(1)∠DCE=90°;(2)![]() ;(3)2BD2=DA2+DC2,证明见解析.
;(3)2BD2=DA2+DC2,证明见解析.
【解析】
(1)由已知条件不难证明△ABD≌△CBE,可得∠A=∠ACB=∠BCE=45°,所以∠DCE=90°;(2)由AB=5可得AC=5![]() ,由AD:DC=2:3可以分别求出AD、CD的长度,进而求出CE的长度,利用勾股定理求出DE的长度即可;(3)由△BDE是等腰直角三角形,可得DE=
,由AD:DC=2:3可以分别求出AD、CD的长度,进而求出CE的长度,利用勾股定理求出DE的长度即可;(3)由△BDE是等腰直角三角形,可得DE=![]() BD,因为AD=CE,所以DE2=DC2+CE2=AD2+CD2,所以2BD2=AD2+CD2.
BD,因为AD=CE,所以DE2=DC2+CE2=AD2+CD2,所以2BD2=AD2+CD2.
(1)∵等腰直角△ABC,
∴AB=AC,∠ABC=90°,∠A=∠ACB=45°,
同理可得:DE=BE,∠DBE=90°,∠BDE=∠BED=45°,
∴∠ABD=∠CBE,
∵在△ABD与△CBE中,
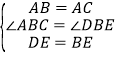 ,
,
∴△ABD≌△CBE,
∴∠A=∠ACB=∠BCE=45°,∠ABD=∠CBE,AD=CE,
∴∠DCE=90°;
(2)当AB=5,AD:DC=2:3时,有AC=![]() ,AD=
,AD=![]() ,DC=
,DC=![]() ,
,
在Rt△DCE中,CD=![]() ,CE=AD=
,CE=AD=![]() ,由勾股定理可得DE=
,由勾股定理可得DE=![]() ;
;
(3)2BD2=DA2+DC2;
∵△BDE是等腰直角三角形,
∴DE=![]() BD,
BD,
∵AD=CE,
∴DE2=DC2+CE2=AD2+CD2,
故2BD2=AD2+CD2.

练习册系列答案
相关题目