题目内容
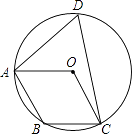
【题目】如图,矩形ABCD中,AB=10,AD=4,点P在边DC上,且△PAB是直角三角形,请在图中标出符合题意的点P,并直接写出PC的长. 
【答案】解:如图,以AB的中点O为圆心,AB的一半5为半径作圆,交CD于点P,点P即为所求; 
设PC=x,则PD=10﹣x,
∵四边形ABCD是矩形,
∴∠D=∠C=90°,
∴∠DAP+∠APD=90°,
∵∠APB=90°,
∴∠APD+∠BPC=90°,
∴∠DAP=∠CPB,
∴△ADP∽△PCB,
∴ ![]() ,即
,即 ![]() ,
,
解得:x=2或x=8,
即PC=2或PC=8
【解析】以AB的中点O为圆心,AB的一半5为半径作圆,交CD于点P,点P即为所求;设PC=x,则PD=10﹣x,证△ADP∽△PCB得 ![]() ,即
,即 ![]() ,解之可得答案.
,解之可得答案.
【考点精析】关于本题考查的矩形的性质和圆周角定理,需要了解矩形的四个角都是直角,矩形的对角线相等;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能得出正确答案.

练习册系列答案
相关题目