题目内容
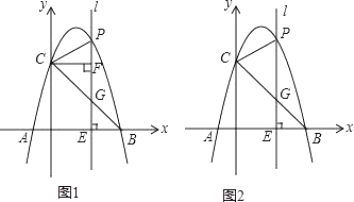
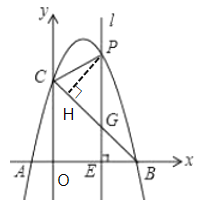
【题目】如图1，抛物线y=﹣x2+bx+c经过A(﹣1，0)，B(4，0)两点，与y轴相交于点C，连接BC，点P为抛物线上一动点，过点P作x轴的垂线l，交直线BC于点G，交x轴于点E．
(1)求抛物线的解析式；
(2)如图1，当P位于y轴右边的抛物线上运动时，过点C作CF⊥直线l，F为垂足，当点P运动到何处时，以P，C，F为顶点的三角形与△OBC相似，并直接写出此时点P的坐标；
(3)如图2，当点P在位于直线BC上方的抛物线上运动时， 连接PB，PC，设点P的横坐标为m， △PBC的面积为S，
①求出S与m的函数关系式；
②求出点P到直线BC的最大距离.
【答案】(1)y=﹣x2+3x+4；(2)点P的坐标为 (2，6)或(4，0)；(3)①S=﹣2m2+8m；②点P到直线BC的最大距离为
.
【解析】
（1）将点A（-1，0），B（4，0）的坐标代入抛物线的解析式，求得b、c的值即可；
（2）先由函数解析式求得点C的坐标，从而得到△OBC为等腰直角三角形，故此当CF=PF时，以P，C，F为顶点的三角形与△OBC相似．设P（t，-t2+3t+4）（t＞0），则CF=t，构建方程从而可求得t的值，于是可求得点P的坐标；
（3）连接EC．设点P的坐标为(m，﹣m2+3m+4)．则OE=m，PE=﹣m2+3m+4，EB=4﹣m．
然后依据S△PBC=S四边形PCEB-S△CEB列出△PBC的面积与m的函数关系式，从而可求得三角形的最大面积，从而求得此时点P坐标，根据坐标求点P到直线BC的最大距离为.
(1)由题意得
，解得
∴抛物线的解析式为y=﹣x2+3x+4．
(2)点P的坐标为 (2，6)或(4，0)．
(3)如图2所示：连接EC．
设点P的坐标为(m，﹣m2+3m+4)．则OE=m，PE=﹣m2+3m+4，EB=4﹣m．
∵C(0，4)，B(4，0)，
∴直线BC的解析式为y=﹣x+4．
∵S四边形PCEB=
OBPE=×4(﹣m2+3m+4)，S△CEB=EBOC=×4×(4﹣m)，
∴S△PBC=S四边形PCEB﹣S△CEB=2(﹣m2+3m+4)﹣2(4﹣m)=﹣2m2+8m．
∵a=﹣2＜0，
∴当a=2时，△PBC的面积S有最大值．
∴P(2，6)，△PBC的面积的最大值为8．
过点P作PH⊥BC于点H，由题意得C（0,4），D(4，0),OB=OC=4，
∴∠ABC=45°=∠EGB，∠PGH=∠EGB=45°，即△PGH是等腰直角三角形，
∵P(2，6),∴OE=2=EB=EG,PG=PE-GE=6-2=4，
∴PH=PG×sin45°=4×
=.
即点P到直线BC的最大距离为.
