Question

【题目】已知二次函数y＝﹣x2+2mx﹣m2+4．

（1）求证：该二次函数的图象与x轴必有两个交点；

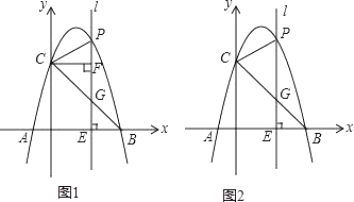
（2）若该二次函数的图象与x轴交于点A、B（点A在点B的左侧），顶点为C，

①求△ABC的面积；

②若点P为该二次函数图象上位于A、C之间的一点，则△PAC面积的最大值为　 　，此时点P的坐标为　 　．

Answer 1

【答案】（1）见解析；（2）①8；②1，（m﹣1，3）

【解析】

（1）根据b2﹣4ac＝4m2﹣4×（﹣1）×（﹣m2+4）＝16＞0，即可证明.

（2）①当y＝0时，﹣x2+2mx﹣m2+4＝0，解得x1＝m+2，x2＝m﹣2，即可求出AB＝4

，将一般式配方为顶点式即可求出顶点为C的坐标，即可求出点△ABC的面积；

②设点P横坐标为（a，b），其中b＝﹣a2+2am﹣m2+4,表示出△PAC面积，整理得S△PAC＝﹣a2+2a（m﹣1）﹣m2+2m，根据二次函数的性质即可求解.

（1）证明：当y＝0时，﹣x2+2mx﹣m2+4＝0，

∵b2﹣4ac＝4m2﹣4×（﹣1）×（﹣m2+4）＝16＞0，

∴此一元二次方程有两个解，

∴该二次函数的图象与x轴必有两个交点；

（2）解：①当y＝0时，﹣x2+2mx﹣m2+4＝0，

解得：x1＝m+2，x2＝m﹣2

∵点A在点B的左侧

∴点A、B横坐标分别为m﹣2，m+2

∴AB＝4

配方得y＝﹣x2+2mx﹣m2+4＝﹣（x﹣m）2+4

∴抛物线顶点为（m，4）

∴S△ABC＝×4×4＝8；

②设点P横坐标为（a，b），其中b＝﹣a2+2am﹣m2+4

整理得S△PAC＝b+2m﹣2a﹣4

把b＝﹣a2+2am﹣m2+4代入上式

S△PAC＝﹣a2+2am﹣m2+4+2m﹣2a﹣4

整理得

S△PAC＝﹣a2+2a（m﹣1）﹣m2+2m

∵a＝﹣1＜0

∴当a＝m﹣1时，△PAC面积最大值为1

此时点P坐标为（m﹣1，3）

故答案为：1，（m﹣1，3）