题目内容
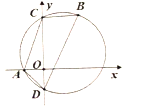
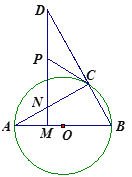
【题目】如图,△ABC的外接圆圆心O在AB上,点D是BC延长线上一点,DM⊥AB于M,交AC于N,且AC=CD.CP是△CDN的边ND上的中线.
(1)求证:AB=DN;
(2)试判断CP与⊙O的位置关系,并证明你的结论;
(3)若PC=5,CD=8,求线段MN的长.
【答案】(1)证明见解析;(2)CP是⊙O的切线,证明见解析.(3)![]() .
.
【解析】
(1)由 AB为⊙O的直径,∠ACB=90°=∠NCD ,再根据角的等量替换得出∠A =∠D
再根据AC=CD,可得△ABC≌△DNC,即可得到AB=DN ;(2)连结OC,根据直角三角形斜边上的中线是斜边的一半,得到PC=PN=![]() ,再得到∠ACO+∠PCN =90°,故∠PCO =90°,即可证明;(3)先得到DN=2PC=10,再利用勾股定理计算出CN=6,由AC=CD=8得到AN-AC-CN=2,再利用sinA=
,再得到∠ACO+∠PCN =90°,故∠PCO =90°,即可证明;(3)先得到DN=2PC=10,再利用勾股定理计算出CN=6,由AC=CD=8得到AN-AC-CN=2,再利用sinA=![]() ,即可求出MN的长度.
,即可求出MN的长度.
解:(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°=∠NCD
∵DM⊥AB,
∴∠AMN=90°,
∴∠ABC+∠A =∠ABC+∠D =90°
∴∠A =∠D
又∵AC=CD,∠ACB=∠NCD
∴△ABC≌△DNC
∴AB=DN
(2)CP是⊙O的切线.
证明:连结OC
∵CP是△CDN的边ND上的中线,∠NCD=90°
∴PC=PN=![]()
∴∠PCN =∠PNC
∵∠ANM=∠PNC
∴∠ANM=∠PCN
∵OA=OC
∴∠A=∠ACO
∵∠A+∠ANM =90°
∴∠ACO+∠PCN =90°
∴∠PCO =90°
∴CP是⊙O的切线
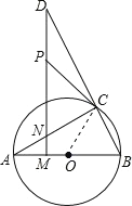
(3)∵PC=5
∴DN=2PC=10
∵△ABC≌△DNC
∴CN=CB,AC=CD=8,AB=DN=10
∴![]()
∴AN=AC-CN=2
∵sinA=![]()
∴![]()
∴![]()

练习册系列答案
相关题目