题目内容
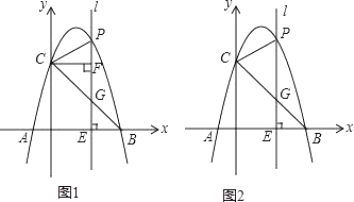
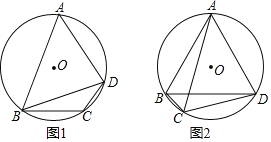
【题目】已知:如图,BC为⊙O的弦,点A为⊙O上一个动点,△OBC的周长为16.过C作CD∥AB交⊙O于D,BD与AC相交于点P,过点P作PQ∥AB交于Q,设∠A的度数为α.
(1)如图1,求∠COB的度数(用含α的式子表示);
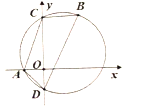
(2)如图2,若∠ABC=90°时,AB=8,求阴影部分面积(用含α的式子表示);
(3)如图1,当PQ=2,求![]() 的值.
的值.

【答案】(1)∠COB=2α;(2)阴影部分面积=![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据圆周角定理可得∠COB=2∠A=2α;
(2)当∠ABC=90°时,可得点P与圆心O重合,根据△OBC的周长为16以及AB=8,可求得⊙O的半径为5,可得出扇形COB的面积以及△OBC的面积,进而得出阴影部分面积;
(3)由CD∥AB∥PQ,可得△BPQ∽△BDC,△CPQ∽△CAB,即,![]() 两式子相加可得
两式子相加可得![]() ,即可得出
,即可得出![]() 的值.
的值.
解:(1)∵∠A的度数为α,
∴∠COB=2∠A=2α,
(2)当∠ABC=90°时,AC为⊙O的直径,
∵CD∥AB,
∴∠DCB=180°﹣90°=90,
∴BD为⊙O的直径,
∴P与圆心O重合,
∵PQ∥AB交于Q,
∴OQ⊥BC,
∴CQ=BQ,
∵AB=8,
∴OQ=![]() AB=4,
AB=4,
设⊙O的半径为r,
∵△OBC的周长为16,
∴CQ=8﹣r,
∴(8﹣r)2+42=r2,
解得r=5,CB=6,
∴阴影部分面积=![]() ;
;
(3)∵CD∥AB∥PQ,
∴△BPQ∽△BDC,△CPQ∽△CAB,
∴![]() ,
,
∴![]() ,
,
∵PQ=2,
∴![]() ,
,
∴![]() =2.
=2.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目