题目内容
【题目】已知在平面直角坐标系xOy中,O为坐标原点,线段AB的两个端点的坐标分别为A (0,2),B(﹣1,0),点C为线段AB的中点,现将线段BA绕点B按逆时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)、经过点D.
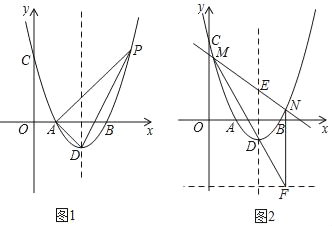
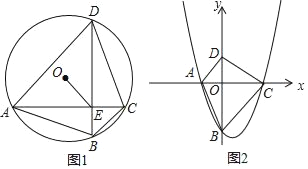
(1)如图1,若该抛物线经过原点O,且a=﹣1.
①求点D的坐标及该抛物线的解析式;
②连结CD,问:在抛物线上是否存在点P,使得∠POB与∠BCD互余?若存在,请求出所有满足条件的点P的坐标,若不存在,请说明理由.
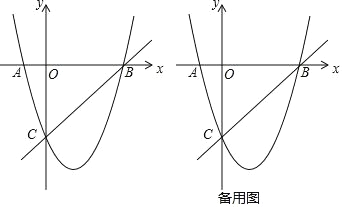
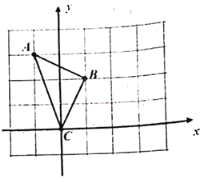
(2)如图2,若该抛物线y=ax2+bx+c(a<0)经过点E(﹣1,1),点Q在抛物线上,且满足∠QOB与∠BCD互余,若符合条件的Q点的个数是4个,请直接写出a的取值范围 .
【答案】(1)①D(﹣3,1),抛物线的表达式为:y=﹣x2﹣![]() x;②存在,点P的坐标为:P(﹣
x;②存在,点P的坐标为:P(﹣![]() ,
,![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() );(2)a<﹣
);(2)a<﹣![]() 或a>1+
或a>1+![]() 或﹣
或﹣![]() <a<1-
<a<1-![]() .
.
【解析】
(1)①为A (0,2),B(-1,0),BA绕点B按逆时针方向旋转90°得到线段BD,把原点坐标、点D坐标、a=-1代入抛物线方程,即可求解;
②如下图所示,∠QOB与∠BCD互余,直线OP的方程为y=-![]() x,将直线方程与抛物线方程联立即可求解,当P在x轴上方时,用同样的方法可以求解;
x,将直线方程与抛物线方程联立即可求解,当P在x轴上方时,用同样的方法可以求解;
(2)把D、E坐标代入抛物线方程,解得:y=ax2+4ax+(3a+1),①当a<0时,若符合条件的Q点的个数是4个,则Q点在x轴上下各2个,则3a+1<0,然后分Q在x轴上方和x轴下方时两种情况即可求解,同样可以求出a>0的情况.
(1)为A (0,2),B(﹣1,0),
①点C为线段AB的中点,则C(-![]() ,1),
,1),
BA绕点B按逆时针方向旋转90°得到线段BD,
则D(﹣3,1),∴DC∥x轴,
把原点坐标、点D坐标、a=﹣1代入抛物线方程,
解得:抛物线的表达式为:y=﹣x2﹣![]() x…①;
x…①;
②如下图所示,∠QOB与∠BCD互余,
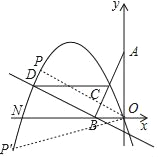
当P在x轴上方时,OP⊥AB,
直线AB的k值为2,则直线OP的k值为﹣![]() ,
,
直线OP的方程为y=﹣![]() x…②,
x…②,
①、②联立并整理得:x=0(舍去),x=﹣![]() ,
,
则点P(﹣![]() ,
,![]() );
);
当P在x轴上方时,
直线OP的方程为y=![]() x…③,
x…③,
①、③联立并整理得:x=0(舍去),x=﹣![]() ,
,
则P′(﹣![]() ,﹣
,﹣![]() );
);
故:存在,点P的坐标为:P(﹣![]() ,
,![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() );
);
(2)把D、E坐标代入抛物线方程,
解得:y=ax2+4ax+(3a+1)…④,
函数与y轴交点的纵坐标为:3a+1
有(2)知:当Q在x轴上方时,OQ的方程为:y=﹣![]() x…⑤,
x…⑤,
当Q在x轴下方时,OQ的方程为:y=![]() x…⑥,
x…⑥,
①当a<0时,若符合条件的Q点的个数是4个,则Q点在x轴上下各2个,则3a+1<0,即:![]() ,
,
Q在x轴上方时,联立④、⑤得:-![]() x=ax2+4ax+(3a+1),△=4a2+
x=ax2+4ax+(3a+1),△=4a2+![]() >0,即:必定有2个Q点,
>0,即:必定有2个Q点,
Q在x轴下方时,联立④、⑥得:x=ax2+4ax+(3a+1),△=4a2﹣8a+![]() >0,a>1+
>0,a>1+![]() 或a<1﹣
或a<1﹣![]() ,
,
故:a<﹣![]() ;
;
②当a<0时,若符合条件的Q点的个数是4个,则Q点在x轴上下各2个,则3a+1>0,即:a>﹣![]() ,
,
Q在x轴上方时,联立④、⑤得:-![]() x=ax2+4ax+(3a+1),△=4a2+
x=ax2+4ax+(3a+1),△=4a2+![]() >0,即:必定有2个Q点,
>0,即:必定有2个Q点,
Q在x轴下方时,联立④、⑥得:x=ax2+4ax+(3a+1),△=4a2﹣8a+![]() >0,a>1+
>0,a>1+![]() 或a<1﹣
或a<1﹣![]() ,
,
故:a>1+![]() 或﹣
或﹣![]() <a<1-
<a<1-![]() .
.
综上所述:a<﹣![]() 或a>1
或a>1![]() 或﹣
或﹣![]() <a<1-
<a<1-![]() .
.

 优学名师名题系列答案
优学名师名题系列答案