题目内容
【题目】定义:如果把一条抛物线绕它的顶点旋转180°得到的抛物线我们称为原抛物线的“孪生抛物线”.
(1)求抛物线y=x-2x的“孪生抛物线”的表达式;
(2)若抛物线y=x-2x+c的顶点为D,与y轴交于点C,其“孪生抛物线”与y轴交于点,请判断△DCC’的形状,并说明理由:
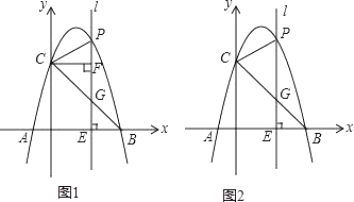
(3)已知抛物线y=x-2x-3与y轴交于点C,与x轴正半轴的交点为A,那么是否在其“孪生抛物线”上存在点P,在y轴上存在点Q,使以点A、C、P、Q为顶点的四边形为平行四边形,若存在,求出P点的坐标;若不存在,说明理由。
【答案】(1)y=-(x-1)=-x+2x-2;(2)等腰Rt△,(3)P1(3,-8),P2(-3,-20).
【解析】
(1)当抛物线绕其顶点旋转180°后,抛物线的顶点坐标不变,只是开口方向相反,则可根据顶点式写出旋转后的抛物线解析式;
(2)可分别求出原抛物线和其“孪生抛物线”与y轴的交点坐标C、C′,由点的坐标可知△DCC’是等腰直角三角形;
(3)可求出A(3,0),C(0,-3),其“孪生抛物线”为y=-x2+2x-5,当AC为对角线时,由中点坐标可知点P不存在,当AC为边时,分两种情况可求得点P的坐标.
(1)抛物线y=x2-2x化为顶点式为y=(x-1)2-1,顶点坐标为(1,-1),由于抛物线y=x2-2x绕其顶点旋转180°后抛物线的顶点坐标不变,只是开口方向相反,
则所得抛物线解析式为y=-(x-1)2-1=-x2+2x-2;
(2)△DCC'是等腰直角三角形,理由如下:
∵抛物线y=x2-2x+c=(x-1)2+c-1,
∴抛物线顶点为D的坐标为(1,c-1),与y轴的交点C的坐标为(0,c),
∴其“孪生抛物线”的解析式为y=-(x-1)2+c-1,与y轴的交点C’的坐标为(0,c-2),
∴CC'=c-(c-2)=2,
∵点D的横坐标为1,
∴∠CDC'=90°,
由对称性质可知DC=DC’,
∴△DCC'是等腰直角三角形;
(3)∵抛物线y=x2-2x-3与y轴交于点C,与x轴正半轴的交点为A,
令x=0,y=-3,令y=0时,y=x2-2x-3,解得x1=-1,x2=3,
∴C(0,-3),A(3,0),
∵y=x2-2x-3=(x-1)2-4,
∴其“孪生抛物线”的解析式为y=-(x-1)2-4=-x2+2x-5,
若A、C为平行四边形的对角线,
∴其中点坐标为(![]() ,
,![]() ),
),
设P(a,-a2+2a-5),
∵A、C、P、Q为顶点的四边形为平行四边形,
∴Q(0,a-3),
∴![]() =
=![]() ,
,
化简得,a2+3a+5=0,△<0,方程无实数解,
∴此时满足条件的点P不存在,
若AC为平行四边形的边,点P在y轴右侧,则AP∥CQ且AP=CQ,
∵点C和点Q在y轴上,
∴点P的横坐标为3,
把x=3代入“孪生抛物线”的解析式y=-32+2×3-5=-9+6-5=-8,
∴P1(3,-8),
若AC为平行四边形的边,点P在y轴左侧,则AQ∥CP且AQ=CP,
∴点P的横坐标为-3,
把x=-3代入“孪生抛物线”的解析式y=-9-6-5=-20,
∴P2(-3,-20)
∴原抛物线的“孪生抛物线”上存在点P1(3,-8),P2(-3,-20),在y轴上存在点Q,使以点A、C、P、Q为顶点的四边形为平行四边形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
销售单价(元) | x |
销售量y(件) |
|
销售玩具获得利润w(元) |
|
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
【题目】阅读材料:
工厂加工某种新型材料,首先要将材料进行加温处理,使这种材料保持在一定的温度范围内方可进行继续加工![]() 处理这种材料时,材料温度
处理这种材料时,材料温度![]() 是时间
是时间![]() 的函数
的函数![]() 下面是小明同学研究该函数的过程,把它补充完整:
下面是小明同学研究该函数的过程,把它补充完整:
![]() 在这个函数关系中,自变量x的取值范围是______.
在这个函数关系中,自变量x的取值范围是______.
![]() 如表记录了17min内10个时间点材料温度y随时间x变化的情况:
如表记录了17min内10个时间点材料温度y随时间x变化的情况:
时间 | 0 | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 |
|
温度 | 15 | 24 | 42 | 60 |
|
|
|
| m |
|
|
上表中m的值为______.
![]() 如图,在平面直角坐标系xOy中,已经描出了上表中的部分点
如图,在平面直角坐标系xOy中,已经描出了上表中的部分点![]() 根据描出的点,画出该函数的图象.
根据描出的点,画出该函数的图象.
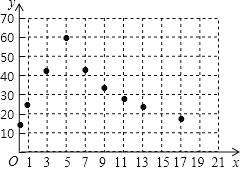
![]() 根据列出的表格和所画的函数图象,可以得到,当
根据列出的表格和所画的函数图象,可以得到,当![]() 时,y与x之间的函数表达式为______,当
时,y与x之间的函数表达式为______,当![]() 时,y与x之间的函数表达式为______.
时,y与x之间的函数表达式为______.
![]() 根据工艺的要求,当材料的温度不低于
根据工艺的要求,当材料的温度不低于![]() 时,方可以进行产品加工,在图中所示的温度变化过程中,可以进行加工的时间长度为______min.
时,方可以进行产品加工,在图中所示的温度变化过程中,可以进行加工的时间长度为______min.