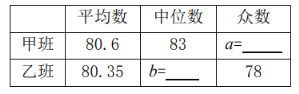
题目内容
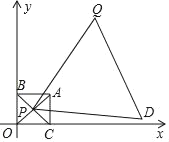
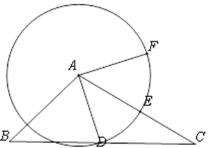
【题目】如图,已知△ABC,AB=![]() ,
,![]() ,∠B=45°,点D在边BC上,联结AD, 以点A为圆心,AD为半径画圆,与边AC交于点E,点F在圆A上,且AF⊥AD.
,∠B=45°,点D在边BC上,联结AD, 以点A为圆心,AD为半径画圆,与边AC交于点E,点F在圆A上,且AF⊥AD.
(1)设BD为x,点D、F之间的距离为y,求y关于x的函数解析式,并写出定义域;
(2)如果E是![]() 的中点,求
的中点,求![]() 的值;
的值;
(3)联结CF,如果四边形ADCF是梯形,求BD的长 .

【答案】(1) ![]() (0≤x≤3); (2)
(0≤x≤3); (2) ![]() ; (3) BD的长是1或
; (3) BD的长是1或![]() .
.
【解析】
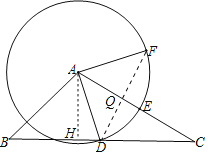
(1)过点A作AH⊥BC,垂足为点H.构造直角三角形,利用解直角三角形和勾股定理求得AD的长度.联结DF,点D、F之间的距离y即为DF的长度,在Rt△ADF中,利用锐角三角形函数的定义求得DF的长度,易得函数关系式.
(2)由勾股定理求得:AC=![]() .设DF与AE相交于点Q,通过解Rt△DCQ和Rt△AHC推知
.设DF与AE相交于点Q,通过解Rt△DCQ和Rt△AHC推知![]() .故设DQ=k,CQ=2k,AQ=DQ=k,所以再次利用勾股定理推知DC的长度,结合图形求得线段BD的长度,易得答案.
.故设DQ=k,CQ=2k,AQ=DQ=k,所以再次利用勾股定理推知DC的长度,结合图形求得线段BD的长度,易得答案.
(3)如果四边形ADCF是梯形,则需要分类讨论:①当AF∥DC、②当AD∥FC.根据相似三角形的判定与性质,结合图形解答.
(1)过点![]() 作AH⊥BC,垂足为点H.
作AH⊥BC,垂足为点H.
∵∠B=45°,AB=![]() ,∴
,∴![]() .
.
∵BD为x,∴![]() .
.
在Rt△![]() 中,
中,![]() ,∴
,∴![]() .
.
联结DF,点D、F之间的距离y即为DF的长度.
∵点F在圆A上,且AF⊥AD,∴![]() ,
,![]() .
.
在Rt△![]() 中,
中,![]() ,∴
,∴![]() .
.
∴![]() .
.![]() ;
;
(2)∵E![]() 的中点,∴
的中点,∴![]() ,
,![]() 平分
平分![]() .
.
∵BC=3,∴![]() .∴
.∴![]() .
.
设DF与AE相交于点Q,在Rt△![]() 中,
中,![]() ,
,![]() .
.
在Rt△![]() 中,
中,![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .
.
设![]() ,
,![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
(3)如果四边形ADCF是梯形
则①当AF∥DC时,![]() .
.
∵![]() ,∴
,∴![]() ,即点D与点H重合. ∴
,即点D与点H重合. ∴![]() .
.
②当AD∥FC时,![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() ∽
∽![]() .∴
.∴![]() .
.
∵![]() ,
,![]() .
.
∴![]() .即
.即![]() ,
,
整理得 ![]() ,解得
,解得 ![]() (负数舍去).
(负数舍去).
综上所述,如果四边形ADCF是梯形,BD的长是1或![]() .
.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案