题目内容
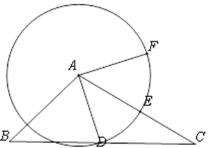
【题目】如图,某底面为圆形的古塔剖面和山坡的剖面在同一平面上,古塔EF(F为塔底的中心)与地面BD垂直,古塔的底面直径CD=8米,BC=10米,斜坡AB=26米,斜坡坡面AB的坡度i=5:12,在坡脚的点A处测得古塔顶端点E的仰角∠GAE=47°,则古塔EF的高度约( )(参考数据:sin47°≈0.73,cos47°≈0.68,tan47°≈1.07)
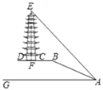
A. 27.74米B. 30.66米C. 35.51米D. 40.66米
【答案】B
【解析】
延长EF交AG于点H,则EH⊥AG,作BP⊥AG,由i=5:12及AB=26可得FH=BP=10,AP=24,继而可知AH=38,利用EH=AHtan∠GAE求得EH的长,继而可得答案.
如图,延长EF交AG于点H,则EH⊥AG,作BP⊥AG于点P,
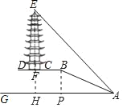
由i=5:12可设BP=5x,则AP=12x,
由BP2+AP2=AB2可得(5x)2+(12x)2=262,
解得:x=2(负值舍去),
则FH=BP=10,AP=24,
∵CF=4,BC=10,
∴HP=BF=14,
∴AH=38,
则EH=AHtan∠GAE=38×tan47°≈40.66,
∴EF=EH﹣FH=40.66﹣10=30.66(米),
故选:B.

【题目】某校八年级两个班,各选派10名学生参加学校举行的“美丽绍兴乡土风情知识”大赛预赛各参赛选手的成绩如下:
八(1)班:88,91,92,93,93,93,94,98,98,100;
八(2)班:89,93,93,93,95,96,96,98,98,99.
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
八(1)班 | 100 | m | 93 | 93 | 12 |
八(2)班 | 99 | 95 | n | 93 | 8.4 |
(1)求表中m、n的值;
(2)依据数据分析表,有同学说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有同学说(2)班的成绩更好请您写出两条支持八(2)班成绩好的理由.