题目内容
【题目】如图,点![]() 的坐标为
的坐标为![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴以每秒
轴以每秒![]() 个单位的速度向上移动,且过点
个单位的速度向上移动,且过点![]() 的直线
的直线![]() 也随之移动,如果点
也随之移动,如果点![]() 关于
关于![]() 的对称点落在坐标轴上,没点
的对称点落在坐标轴上,没点![]() 的移动时间为
的移动时间为![]() ,那么
,那么![]() 的值可以是___.
的值可以是___.

【答案】2或3(答一个即可)
【解析】
找出点M关于直线l在坐标轴上的对称点E、F,如图所示.求出点E、F的坐标,然后分别求出ME、MF中点坐标,最后分别求出时间t的值.
如图,过点M作MF⊥直线l,交y轴于点F,交x轴于点E,则点E.F为点M在坐标轴上的对称点.
过点M作MD⊥x轴于点D,则OD=3,MD=2.
由直线l:y=x+b可知∠PDO=∠OPD=45°,
∴∠MED=∠OEF=45°,则△MDE与△OEF均为等腰直角三角形,
∴DE=MD=2,OE=OF=1,
∴E(1,0),F(0,1).
∵M(3,2),F(0,1),
∴线段MF中点坐标为(![]() ,
,![]() ).
).
直线y=x+b过点(![]() ,
,![]() ),则
),则![]() =
=![]() +b,解得:b=2,
+b,解得:b=2,
∴t=2.
∵M(3,2),E(1,0),
∴线段ME中点坐标为(2,1).
直线y=x+b过点(2,1),则1=2+b,解得:b=3,
∴t=3.
故点M关于l的对称点,当t=2时,落在y轴上,当t=3时,落在x轴上,
故答案为2或3.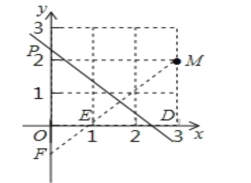

【题目】某校八年级两个班,各选派10名学生参加学校举行的“美丽绍兴乡土风情知识”大赛预赛各参赛选手的成绩如下:
八(1)班:88,91,92,93,93,93,94,98,98,100;
八(2)班:89,93,93,93,95,96,96,98,98,99.
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
八(1)班 | 100 | m | 93 | 93 | 12 |
八(2)班 | 99 | 95 | n | 93 | 8.4 |
(1)求表中m、n的值;
(2)依据数据分析表,有同学说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有同学说(2)班的成绩更好请您写出两条支持八(2)班成绩好的理由.