题目内容
【题目】如图,在平面直角坐标系中,四边形ABOC是正方形,点A的坐标为(1,1),弧AA1是以点B为圆心,BA为半径的圆弧;弧A1A2是以点O为圆心,OA2为半径的圆弧;弧A2A3是以点C为圆心,CA2为半径的圆弧;弧A3A4是以点A为圆心,AA3为半径的圆弧,继续以点B、O、C、A为圆心,按上述作法得到的曲线AA1A2A3A4A5…称为正方形的“渐开线”,则点A2019的坐标是_____.
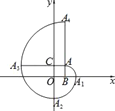
【答案】(﹣2019,1)
【解析】
根据画弧的方法以及罗列部分点的坐标发现:点Ax的坐标满足“A4n=(1,4n+1),A4n+1=(4n+2,0),A4n+2=(0,-(4n+2)),A4n+3=(-(4n+3),1)”,根据这一规律即可得出A2019点的坐标.
观察,找规律:A(1,1),A1(2,0),A2(0,﹣2),A3(﹣3,1),A4(1,5),A5(6,0),A6(0,﹣6),A7(﹣7,1),A8(1,9)…,
∴A4n=(1,4n+1),A4n+1=(4n+2,0),A4n+2=(0,﹣(4n+2)),A4n+3=(﹣(4n+3),1).
∵2019=504×4+3,
∴A2019的坐标为(﹣2019,1).
故答案为:(﹣2019,1).

【题目】某校八年级两个班,各选派10名学生参加学校举行的“美丽绍兴乡土风情知识”大赛预赛各参赛选手的成绩如下:
八(1)班:88,91,92,93,93,93,94,98,98,100;
八(2)班:89,93,93,93,95,96,96,98,98,99.
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
八(1)班 | 100 | m | 93 | 93 | 12 |
八(2)班 | 99 | 95 | n | 93 | 8.4 |
(1)求表中m、n的值;
(2)依据数据分析表,有同学说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有同学说(2)班的成绩更好请您写出两条支持八(2)班成绩好的理由.