题目内容
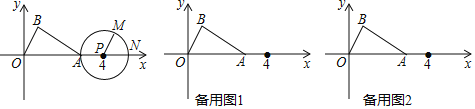
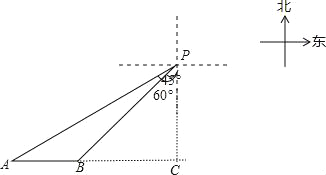
【题目】一艘轮船位于灯塔P南偏西60°方向,距离灯塔20海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:![]() ≈1.732,结果精确到0.1)?
≈1.732,结果精确到0.1)?
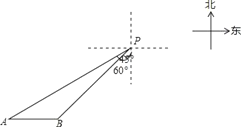
【答案】它向东航行约7.3海里到达灯塔P南偏西45°方向上的B处.
【解析】
利用题意得到AC⊥PC,∠APC=60°,∠BPC=45°,AP=20,如图,在Rt△APC中,利用余弦的定义计算出PC=10,利用勾股定理求出AC,再判断△PBC为等腰直角三角形得到BC=PC=10,然后计算AC-BC即可.
如图,AC⊥PC,∠APC=60°,∠BPC=45°,AP=20,
在Rt△APC中,∵cos∠APC=![]() ,
,
∴PC=20cos60°=10,
∴AC=![]() =10
=10![]() ,
,
在△PBC中,∵∠BPC=45°,
∴△PBC为等腰直角三角形,
∴BC=PC=10,
∴AB=AC﹣BC=10![]() ﹣10≈7.3(海里),
﹣10≈7.3(海里),
答:它向东航行约7.3海里到达灯塔P南偏西45°方向上的B处.

练习册系列答案
相关题目