题目内容
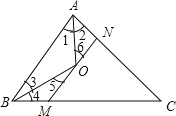
【题目】如图，已知△ABC中，AC+BC=24，AO，BO分别是角平分线，且MN∥BA，分别交AC于N，BC于M，则△CMN的周长为（ ）
A.12 B.24 C.36 D.不确定
【答案】B
【解析】
试题分析：由AO，BO分别是角平分线求得∠1=∠2，∠3=∠4，利用平行线性质求得，∠1=∠6，∠3=∠5，利用等量代换求得∠2=∠6，∠4=∠5，即可解题．
解：由AO，BO分别是角平分线得∠1=∠2，∠3=∠4，
又∵MN∥BA，∴∠1=∠6，∠3=∠5，
∴∠2=∠6，∠4=∠5，
∴AN=NO，BM=OM．
∵AC+BC=24，∴AC+BC=AN+NC+BM+MC=24，
即MN+MC+NC=24，也就是△CMN的周长是24．
故选B．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
【题目】下表是一组二次函数y＝x2+3x﹣5的自变量x与函数值y的对应值：
x | 1 | 1.2 | 1.3 | 1.4 |
y | ﹣1 | 0.04 | 0.59 | 1.16 |
那么方程x2+3x﹣5＝0的一个近似根是（ ）
A.1B.1.1C.1.2D.1.3