题目内容
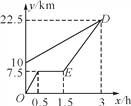
【题目】(本题满分7分)小亮、小明两人星期天8：00同时分别从A，B两地出发，沿同一条路线前往新华书店C.小明从B地步行出发，小亮骑自行车从A地出发途经B地，途中自行车发生故障，维修耽误了1 h，结果他俩11：00同时到达书店C.下图是他们距离A地的路程y(km)与所用时间x(h)之间的函数关系图象．请根据图中提供的信息，解答下列问题：
(1)求图中直线DE的函数解析式；
(2)若小亮的自行车不发生故障，且保持出发时的速度前行，则他出发多久可追上小明？此时他距离A地多远？
【答案】(1) DE的函数解析式为y＝10x－7.5 ；(2) 出发
h可追上小明，此时他距离A地
km.
【解析】解：(1)设直线DE的函数解析式为y＝kx＋b.易知点D的坐标为(3，22.5)，点E的坐标为(1.5，7.5)，∴
解得
∴直线DE的函数解析式为y＝10x－7.5 (2)小明的速度为(22.5－10)÷3＝
(km/h)．小亮出发时的速度为7.5÷0.5＝15(km/h)．设小亮出发m小时后追上小明，由题意，得m＋10＝15m，解得m＝
，当m＝时，15×＝
(km)．答：若小亮的自行车不发生故障，且保持出发时的速度前行，则他出发
h可追上小明，此时他距离A地km
练习册系列答案
相关题目
