题目内容
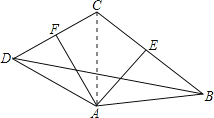
【题目】如图所示,四边形ABCD中,AE、AF分别是BC、CD的垂直平分线,∠EAF=80°,∠CBD=30°,则∠ADC的度数为( )

A. 45° B. 60°
C. 80° D. 100°
【答案】B
【解析】连接AC,
∵AE、AF分别是BC、CD的垂直平分线,
∴AB=AC=AD,
∵AF⊥DC,AE⊥BC,
∴∠CAF=∠DAF,∠CAE=∠BAE.
∴∠DAB=2∠EAF=160°,
∴∠ABD=(180°-160°)÷2=10°,
∴∠ABC=∠ACB=30°+10°=40°;
在四边形AECF中,
∠FCE=360°-90°-90°-80°=100°,
∴∠ACD=100°-40°=60°,
∴∠ADC=∠ACD=60°,
故选B.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目