题目内容
【题目】如图1,在△ABC中,AC=BC,∠ACB=90°,CE与AB相交于点D,且BE⊥CE,AF⊥CE,垂足分别为点E、F.
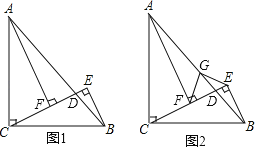
(1)若AF=5,BE=2,求EF的长.
(2)如图2,取AB中点G,连接FC、EC,请判断△GEF的形状,并说明理由.
【答案】(1)EF=3;(2)△GEF为等腰直角三角形;理由见解析.
【解析】
(1)证得∠ACF=∠CBE,由AAS证得△ACF≌△CBE得出CF=BE=2,AF=CE=5,即可得出结果;
(2)连接CG,证得CG⊥AB,∠BCG=![]() ∠ACB=45°,则∠CBG=45°,推出∠GCB=∠CBG=45°,得出CG=BG,易证∠FAD=∠EBG,由△ACF≌△CBE得出CF=BE,∠CAF=∠BCE,证出∠FAD=∠GCD,∠EBG=∠FCG,由SAS证得△CFG≌△BEG得出FG=EG,∠CGF=∠EGB,由∠CGF+∠FGD=90°,得出∠FGD+∠EGB=90°,即∠FGE=90°,即可得出结论.
∠ACB=45°,则∠CBG=45°,推出∠GCB=∠CBG=45°,得出CG=BG,易证∠FAD=∠EBG,由△ACF≌△CBE得出CF=BE,∠CAF=∠BCE,证出∠FAD=∠GCD,∠EBG=∠FCG,由SAS证得△CFG≌△BEG得出FG=EG,∠CGF=∠EGB,由∠CGF+∠FGD=90°,得出∠FGD+∠EGB=90°,即∠FGE=90°,即可得出结论.
(1)∵BE⊥CE,
∴∠BEC=90°,
∵∠ACB=90°,
∴∠BEC=∠ACB,
∴∠ACF+∠BCE=∠BCE+∠CBE=90°,
∴∠ACF=∠CBE,
∵AF⊥CE,
∴∠AFC=90°,
在△ACF和△CBE中,
∵∠ACF=∠CBE,∠AFC=∠BEC,AC=BC,
∴△ACF≌△CBE(AAS),
∴CF=BE=2,AF=CE=5,
∵EF=CE﹣CF,
∴EF=5﹣2=3;
(2)△GEF为等腰直角三角形;理由如下:

连接CG,如图2所示:
∵AC=BC,AG=BG,
∴CG⊥AB,∠BCG=![]() ∠ACB=
∠ACB=![]() ×90°=45°,
×90°=45°,
∴∠CBG=90°﹣45°=45°,
∴∠GCB=∠CBG=45°,
∴CG=BG,
在△ADF和△BDE中,∵∠AFD=∠BED,
∴∠FAD=∠EBG,
由(1)证可知:△ACF≌△CBE,
∴CF=BE,∠CAF=∠BCE,
∵∠CAF+∠FAD=∠GCD+∠BCE=45°,
∴∠FAD=∠GCD,
∴∠EBG=∠FCG,
在△CFG与△BEG中,
∵CG=BG,∠FCG=∠EBG,CF=BE,
∴△CFG≌△BEG(SAS),
∴FG=EG,∠CGF=∠EGB,
∵∠CGF+∠FGD=90°,
∴∠FGD+∠EGB=90°,即∠FGE=90°,
∴△FGE是等腰直角三角形.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案