题目内容
【题目】如图,在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA.
(1)求证:∠BAD=∠EDC;
(2)作出点E关于直线BC的对称点M,连接DM、AM,猜想DM与AM的数量关系,并说明理由.

【答案】(1)见解析;(2) 猜想:DM=AM. 理由见解析.
【解析】
(1)根据等边三角形的性质得出相等的角,相等的边,再等量代换即可得证;
(2)根据题意画出图形,根据轴对称的性质,得∠MDC=∠EDC,DE=DM,然后根据(1)的结论和等边三角形的性质证明即可.
(1)证明:∵△ABC是等边三角形,∴∠BAC=∠ACB=60°.
又∵∠BAD+∠DAC=∠BAC,∠EDC+∠DEC=∠ACB,
∴∠BAD+∠DAC=∠EDC+∠DEC.
∵DE=DA,∴∠DAC=∠DEC,
∴∠BAD=∠EDC.
(2)解:按题意画图如图所示.
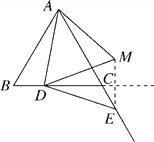
猜想:DM=AM.
理由如下:∵点M、E关于直线BC对称,
∴∠MDC=∠EDC,DE=DM.
又由(1)知∠BAD=∠EDC,∴∠MDC=∠BAD.
∵∠ADC=∠BAD+∠B,即∠ADM+∠MDC=∠BAD+∠B,
∴∠ADM=∠B=60°.
又∵DA=DE=DM,
∴△ADM是等边三角形,
∴DM=AM.

练习册系列答案
相关题目