题目内容
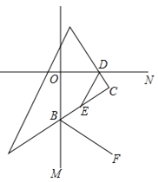
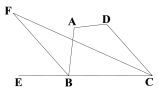
【题目】如图,四边形ABCD的内角∠DCB与外角∠ABE的平分线相交于点F.
(1)若BF∥CD,∠ABC=80°,求∠DCB的度数;
(2)已知四边形ABCD中,∠A=105,∠D=125,求∠F的度数;
(3)猜想∠F、∠A、∠D之间的数量关系,并说明理由.
【答案】(1)50°;(2)25°;(3)∠F=(∠A+∠D-180)°.
【解析】
(1)由∠ABC=80°,可知∠ABE=100°,根据BF平分∠ABE,BF∥CD可得∠BCD=50°.
(2)由三角形外角性质可知∠F=∠FBE-∠FCE,而BF平分∠ABE、CF平分∠BCD,故∠F=![]() (∠ABE-∠FCE),由补角性质和四边形内角和可得∠ABE=360°-∠A-∠B-∠BCD,将已知代入即可求解;
(∠ABE-∠FCE),由补角性质和四边形内角和可得∠ABE=360°-∠A-∠B-∠BCD,将已知代入即可求解;
(3)同(2)可得∠F=![]() (∠A+∠D-180°)
(∠A+∠D-180°)
解:(1)∵∠ABC=80°,
∴∠ABE=180°-∠ABC=100°,
∵BF平分∠ABE,
∴∠EBF=![]() ∠ABE=50°,
∠ABE=50°,
∵BF∥CD
∴∠BCD=∠EBF=50°;
(2)∵∠FBE是△EBC的外角,
∴∠F=∠EBF-∠ECF
∵BF平分∠ABE、CF平分∠BCD,
∴∠EBF=![]() ∠ABE=,∠ECF=
∠ABE=,∠ECF=![]() ∠BCD,
∠BCD,
∵∠ABE=180°-∠ABC,
∴∠F=![]() (180°-∠ABC)-
(180°-∠ABC)-![]() ∠BCD=
∠BCD=![]() [180°-(∠ABC+∠BCD)],
[180°-(∠ABC+∠BCD)],
∵在四边形ABCD中,∠ABC+∠BCD=360°-∠A-∠D,
∴∠F=![]() [180°-(360°-∠A-∠D)],
[180°-(360°-∠A-∠D)],
∴∠F=![]() (∠A+∠D-180°),
(∠A+∠D-180°),
∵∠A=105,∠D=125,
∴∠F=![]() (105 +125 -180°)=25°,
(105 +125 -180°)=25°,
(3)结论:∠F=![]() (∠A+∠D-180°)
(∠A+∠D-180°)
理由如下:∵∠FBE是△EBC的外角,
∴∠F=∠EBF-∠ECF
∵BF平分∠ABE、CF平分∠BCD,
∴∠EBF=![]() ∠ABE=,∠ECF=
∠ABE=,∠ECF=![]() ∠BCD,
∠BCD,
∵∠ABE=180°-∠ABC,
∴∠F=![]() (180°-∠ABC)-
(180°-∠ABC)-![]() ∠BCD=
∠BCD=![]() [180°-(∠ABC+∠BCD)],
[180°-(∠ABC+∠BCD)],
∵在四边形ABCD中,∠ABC+∠BCD=360°-∠A-∠D,
∴∠F=![]() [180°-(360°-∠A-∠D)],
[180°-(360°-∠A-∠D)],
∴∠F=![]() (∠A+∠D-180°),
(∠A+∠D-180°),

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案