��Ŀ����
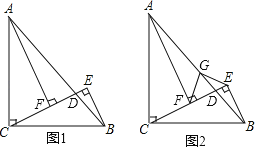
����Ŀ����ͼ����֪���ij���ODΪ18 m��λ�������ߴ������ĸ߶�ABΪ2.4 m��һ��Ավ�ڵ�O����������ӵ�O�����Ϸ�1.6 m��C������ǰ���ɳ������������������O��ˮƽ����OEΪ6 mʱ��������ߵ�G������ͼ��ʾ��ƽ��ֱ������ϵ
(1) �������������߶�Ϊ3.4 mʱ���Է���������0.4 m�ĵ�F����һ��Ա��������������߶�Ϊ3.1 m����������Ƿ���������ɹ�����ͨ������˵��
(2) ����Ա�����Ҫ���������ֲ����߽磬��������е����߶�h��ȡֵ��Χ�Ƕ��٣�������ѹ������û���磩

���𰸡���1�����������ɹ������ɼ���������2��h��3.025
��������
��1�����ݴ�ʱ�����߶�������Ϊ��6��3.4���������ʽΪy=a��x��6��2+3.4���ٽ���C������뼴����ã��ɽ���ʽ���x=9.4ʱy��ֵ����������������߶�Ϊ3.1�ױȽϼ��ɵã�
��2���������߽���ʽΪy=a��x��6��2+h������C�������õ���h��ʾa��ʽ�ӣ��ٸ������Ҫ���������ֲ����߽缴x=9ʱ��y��2.4��x=18ʱ��y��0�ó�����h�IJ���ʽ�飬��֮���ɵã�
��1����������֪��ʱ�����ߵĶ���G������Ϊ��6��3.4����
�������߽���ʽΪy=a��x��6��2+3.4��
����C��0��1.6�����룬�ã�36a+3.4=1.6��
��ã�a=��![]() ��
��
��������еĸ߶�y��ˮƽ����x�ĺ�����ϵʽΪy=��![]() ��x��6��2+
��x��6��2+![]() ��
��
�����x=9.5ʱ��y=��![]() ��9.4��6��2+
��9.4��6��2+![]() ��2.8��3.1��
��2.8��3.1��
����������������ɹ���
��3���������߽���ʽΪy=a��x��6��2+h��
����C��0��1.6�����룬�ã�36a+h=1.6����a=![]() ��
��
���ʱ�����߽���ʽΪy=![]() ��x��6��2+h��
��x��6��2+h��
�������⣬�ã� ��
��
��ã�h��3.025��
��������е����߶�h��ȡֵ��Χ��h��3.025��