题目内容
【题目】“全民防控新冠病毒”期间某公司推出一款消毒产品,成本价8元/千克,经过市场调查,该产品的日销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)之间满足一次函数关系,该产品的日销售量与销售单价几组对应值如表:
(元/千克)之间满足一次函数关系,该产品的日销售量与销售单价几组对应值如表:
销售单价 | 12 | 16 | 20 | 24 |
日销售量 | 220 | 180 | 140 |
|
(注:日销售利润![]() 日销售量
日销售量![]() (销售单价
(销售单价![]() 成本单价)
成本单价)
(1)求![]() 关于
关于![]() 的函数解析式(不要求写出
的函数解析式(不要求写出![]() 的取值范围);
的取值范围);
(2)根据以上信息,填空:
①![]() _______千克;
_______千克;
②当销售价格![]() _______元时,日销售利润
_______元时,日销售利润![]() 最大,最大值是_______元;
最大,最大值是_______元;
(3)该公司决定从每天的销售利润中捐赠100元给“精准扶贫”对象,为了保证捐赠后每天的剩余利润不低于1500元,试确定该产品销售单价的范围.
【答案】(1)![]() ;(2)①100;②21,1690;(3)该产品销售单价的范围为
;(2)①100;②21,1690;(3)该产品销售单价的范围为![]() .
.
【解析】
(1)设y关于x的函数解析式为y=kx+b,由待定系数法求解即可;
(2)①将x=24代入一次函数解析式,计算即可得出m的值;②根据日销售利润=日销售量×(销售单价-成本单价)写出函数关系式,并将其配方,写成顶点式,按照二次函数的性质可得答案;
(3)根据题意,W=-10x2+420x-2720-100≥1500,变形得出关于x的不等式,再根据二次函数的性质可得答案.
解:(1)设y关于x的函数解析式为y=kx+b,将(12,220),(16,180)代入得:
![]() ,解得
,解得![]() .
.
∴y=-10x+340;
(2)①∵当x=24时,y=-10×24+340=100,
∴m=100.
故答案为:100;
②由题意得:
W=(-10x+340)(x-8)=-10x2+420x-2720=-10(x-21)2+1690,
∵-10<0,
∴当x=21时,W有最大值为1690元.
故答案为:21,1690;
(3)由题意得:
W=-10x2+420x-2720-100≥1500,
∴x2-42x+432≤0,
当x2-42x+432=0时,
解得:x1=18,x2=24,
∵函数y=x2-42x+432的二次项系数为正,图象开口向上,
∴18≤x≤24,
∴该产品销售单价的范围为18≤x≤24.

【题目】小魏探究学习函数的经验,对函数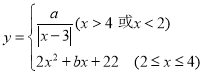 的图像与性质进行了研究,下面是小魏的探究过程,请补充完整.
的图像与性质进行了研究,下面是小魏的探究过程,请补充完整.
(1)下表是![]() 与
与![]() 的几组对应值:
的几组对应值:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
请直接写出:![]() _______,
_______,![]() ______,
______,![]() _______.
_______.
(2)画出该函数图像.
(3)写出该函数的一条性质:_______________.
(4)一次函数![]() 与该函数图像至少有三个交点,则
与该函数图像至少有三个交点,则![]() 的范围_______.
的范围_______.
【题目】某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
商品 | 甲 | 乙 |
进价(元/件) |
|
|
售价(元/件) | 200 | 100 |
若用360元购进甲种商品的件数与用180元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价是多少元?
(2)若超市销售甲、乙两种商品共50件,其中销售甲种商品为![]() 件(
件(![]() ),设销售完50件甲、乙两种商品的总利润为
),设销售完50件甲、乙两种商品的总利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式,并求出
之间的函数关系式,并求出![]() 的最小值.
的最小值.
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为每次连续接球10个,每垫球到位1个记1分.
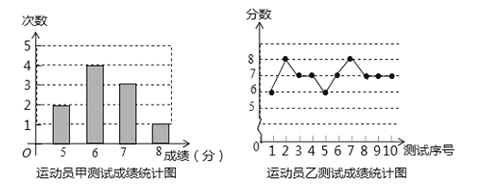
运动员丙测试成绩统计表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 |
| 7 | 5 | 8 |
| 8 | 7 |
运动员丙测试成绩的平均数和众数都是7,
(1)成绩表中的![]() __________,
__________,![]() _________;
_________;
(2)若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?请用你所学过的统计量加以分析说明(参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球从乙手中传出,球传一次甲得到球的概率是____.