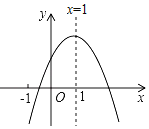ĚâÄżÄÚČÝ
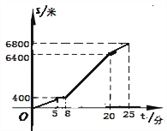
ĄžĚâÄżĄżľćÇňĘÇĹĹÇňśÓłŁšćŃľÁˇľÄÖŘŇŞĎîÄżÖŽŇťŁŽĎÂÁĐÍźąíÖĐľÄĘýžÝĘǟץ˘ŇŇĄ˘ąűČýČËĂżČËĘŽ´ÎľćÇň˛âĘԾijɟ¨ŁŽ˛âĘÔšćÔňÎŞĂż´ÎÁŹĐř˝ÓÇň10¸öŁŹĂżľćÇňľ˝Îť1¸öźÇ1ˇÖŁŽ
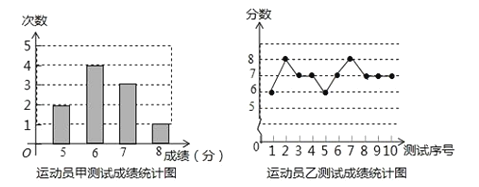
ÔËśŻÔąąű˛âĘԳɟ¨ÍłźĆąí
˛âĘÔĐňşĹ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
łÉź¨Ł¨ˇÖŁŠ | 7 | 6 | 8 |
| 7 | 5 | 8 |
| 8 | 7 |
ÔËśŻÔąąű˛âĘԳɟ¨ľÄĆ˝žůĘýşÍÖÚĘýśźĘÇ7ŁŹ
Ł¨1ŁŠłÉź¨ąíÖĐľÄ![]() __________ŁŹ
__________ŁŹ![]() _________Łť
_________Łť
Ł¨2ŁŠČôÔÚËűĂÇČýČËÖĐŃĄÔńҝΝľćÇňłÉź¨ÓĹĐăÇŇ˝ĎÎŞÎČś¨ľÄ˝ÓÇňÄÜĘÖ×÷ÎŞ×ÔÓÉČËŁŹÄăČĎΪѥ˸üşĎĘĘŁżÇëÓĂÄăËůѧšýľÄÍłźĆÁżźÓŇÔˇÖÎöËľĂ÷Ł¨˛ÎżźĘýžÝŁşČýČ˳ɟ¨ľÄˇ˝˛îˇÖąđÎŞ![]() Ą˘
Ą˘![]() Ą˘
Ą˘![]() ŁŠ
ŁŠ
Ł¨3ŁŠź×Ą˘ŇŇĄ˘ąűČýČËĎ໥֮źä˝řĐĐľćÇňÁˇĎ°ŁŹĂż¸öČËľÄÇňśźľČżÉÄܾĴŤ¸řĆäËűÁ˝ČËŁŹÇň´ÓŇŇĘÖÖĐ´ŤłöŁŹÇň´ŤŇť´Îź×ľĂľ˝ÇňľÄ¸ĹÂĘĘÇ____ŁŽ
Ąž´đ°¸ĄżŁ¨1ŁŠa=7,b=7ŁťŁ¨2ŁŠŃĄŇŇÔËśŻÔą¸üşĎĘĘŁťŁ¨3ŁŠ![]()
Ąž˝âÎöĄż
Ł¨1ŁŠ¸ůžÝÖÚĘýĄ˘ľĂľ˝aĄ˘bÖĐÖÁÉŮÓĐŇť¸öÎŞ7ŁŹÔٸůžÝĆ˝žůĘý˝řśřȡś¨a=b=7Łť
Ł¨2ŁŠÇółöź×Ą˘ŇŇĄ˘ąűľÄĆ˝žůĘýĄ˘ÖÚĘýŁŹÍ¨šýĆ˝žůĘýĄ˘ÖÚĘýąČ˝ĎľĂłöŇŇĄ˘ąű˝ĎşĂŁŹÔٸůžÝˇ˝˛îŁŹľĂłöŇҾijɟ¨˝ĎşĂŁŹ˝ĎÎČś¨Łť
Ł¨3ŁŠÇň´ÓŇŇĘÖÖĐ´ŤłöŁŹÔň´Ť¸řź×ŁŹąűÁ˝Č˾ĸĹÂĘĎŕÍŹŁŹ´ÓśřÇółö¸ĹÂĘŁŽ
˝âŁşŁ¨1ŁŠÓÉÖÚĘýľÄŇâŇĺżÉÖŞŁŹaĄ˘bÖĐÖÁÉŮÓĐŇť¸öÎŞ7ŁŹÓÖŇňÎŞĆ˝žůĘýĘÇ7ŁŹ
ź´Ł¨56+a+bŁŠĄÂ10=7ŁŹ
Ňň´Ëa=7ŁŹb=7ŁŹ
šĘ´đ°¸ÎŞŁş7ŁŹ7Łť
Ł¨2ŁŠź×ľÄĆ˝žůˇÖÎŞŁş![]() ˇÖŁŹÖÚĘýĘÇ6ˇÖŁŹ
ˇÖŁŹÖÚĘýĘÇ6ˇÖŁŹ
ŇŇľÄĆ˝žůˇÖÎŞŁş![]() ˇÖŁŹÖÚĘýĘÇ7ˇÖŁŹ
ˇÖŁŹÖÚĘýĘÇ7ˇÖŁŹ
ąűľÄĆ˝žůˇÖÎŞŁş![]() ŁŹÖÚĘýĘÇ7ˇÖŁŹ
ŁŹÖÚĘýĘÇ7ˇÖŁŹ
´ÓĆ˝žůĘýÉĎż´ŁŹŇŇĄ˘ąűľÄ˝Ď¸ßŁŹ´ÓÖÚĘýÉĎż´ŇŇĄ˘ąű˝Ď¸ßŁŹ
Ąß![]() Ą˘
Ą˘![]() ŁŹ
ŁŹ
Ąŕ![]() Łź
Łź![]() ŁŹ
ŁŹ
ŇҾijɟ¨¸üźÓÎČś¨ŁŹ
šĘŃĄŇŇÔËśŻÔą¸üşĎĘĘŁť
Ł¨3ŁŠÇň´ÓŇŇĘÖÖĐ´ŤłöŁŹÔň´Ť¸řź×ŁŹąűÁ˝Č˾ĸĹÂĘĎŕÍŹŁŹ
ĄŕÇň´ÓŇŇĘÖÖĐ´ŤłöŁŹÇň´ŤŇť´Îź×ľĂľ˝ÇňľÄ¸ĹÂĘĘÇP=![]() .
.

ĄžĚâÄżĄżÎŞÁˡ˘ŐšŃ§ÉúľÄĘýѧşËĐÄËŘŃřŁŹĹŕŃřѧÉúľÄ×ŰşĎÄÜÁŚŁŹÄłĘĐżŞŐšÁËłőČýѧÉúľÄĘýѧ ѧҾˎƽ˛âĘÔ.ÔÚŐâ´Î˛âĘÔÖĐŁŹ´Óź×Ą˘ŇŇÁ˝ĐŁ¸÷ËćťúłéČĄÁË 30 ĂűѧÉúľÄ˛âĘԳɟ¨˝řĐĐľ÷˛éˇÖÎö
ĘŐźŻĘýžÝ
ź×ĐŁ | 94 | 82 | 77 | 76 | 77 | 88 | 90 | 88 | 85 | 86 | 88 | 89 | 84 | 92 | 87 |
88 | 80 | 53 | 89 | 91 | 91 | 86 | 68 | 75 | 94 | 84 | 76 | 69 | 83 | 92 | |
ŇŇĐŁ | 83 | 64 | 91 | 88 | 71 | 92 | 88 | 92 | 86 | 61 | 78 | 91 | 84 | 92 | 92 |
74 | 75 | 93 | 82 | 57 | 86 | 89 | 89 | 94 | 83 | 84 | 81 | 94 | 72 | 90 |
ŐűŔíĄ˘ĂčĘöĘýžÝ °´ČçĎ¡ÖĘýśÎŐűŔíĄ˘ĂčĘöŐâÁ˝×éŃůąžĘýžÝŁş
ČËĘý łÉź¨ x ѧУ | 50ĄÜxĄÜ59 | 60ĄÜxĄÜ69 | 70ĄÜxĄÜ79 | 80ĄÜxĄÜ89 | 90ĄÜxĄÜ100 |
ź×ĐŁ | 1 | 2 | 5 | 15 | 7 |
ŇŇĐŁ | 1 | 2 | 10 |
Ł¨ËľĂ÷ŁşłÉź¨ 80 ˇÖź°ŇÔÉĎÎŞÓĹĐ㣏60~79 ˇÖÎŞşĎ¸ńŁŹ60 ˇÖŇÔĎÂÎŞ˛ťşĎ¸ńŁŠ ˇÖÎöĘýžÝ Á˝×éŃůąžĘýžÝľÄĆ˝žůĘýĄ˘ÖĐÎťĘýĄ˘ÖÚĘýČçĎÂąíËůĘžŁş
ѧУ | Ć˝žůĘý | ÖĐÎťĘý | ÖÚĘý |
ź×ĐŁ | 83.4 | 86 | 88 |
ŇŇĐŁ | 83.2 |
Ł¨1ŁŠÇëÄ㲚ȍąí¸ńŁť
Ł¨2ŁŠČôź×ĐŁÓĐ 300 ĂűѧÉúŁŹšŔźĆź×ĐŁ´Ë´Î˛âĘÔľÄÓĹĐăČËĘýÎŞ Łť
Ł¨3ŁŠżÉŇÔÍƜϳö УѧÉúľÄłÉź¨ąČ˝ĎşĂŁŹŔíÓÉÎŞ ŁŽ
ĄžĚâÄżĄżĐĄĂ÷¸ůžÝѧϰşŻĘýľÄžŃ飏śÔşŻĘýy=x+![]() ľÄÍźĎóÓëĐÔÖĘ˝řĐĐÁËĚ˝žżŁŽ
ľÄÍźĎóÓëĐÔÖĘ˝řĐĐÁËĚ˝žżŁŽ
ĎÂĂćĘÇĐĄĂ÷ľÄĚ˝žżšýłĚŁŹÇ벚łäÍęŐűŁş
Ł¨1ŁŠşŻĘýy=x+![]() ľÄ×ÔąäÁżxľÄČĄÖľˇśÎ§ĘÇ_____ŁŽ
ľÄ×ÔąäÁżxľÄČĄÖľˇśÎ§ĘÇ_____ŁŽ
Ł¨2ŁŠĎÂąíÁĐłöÁËyÓëxľÄź¸×éśÔÓŚÖľŁŹÇëĐ´łömŁŹnľÄÖľŁşm=_____ŁŹn=_____Łť
x | Ą | Š3 | Š2 | Š1 | Š | Š |
|
| 1 | 2 | 3 | 4 | Ą |
y | Ą | Š | Š | Š2 | Š | Š | m |
| 2 |
| n |
| Ą |
Ł¨3ŁŠČçÍźŁŹÔÚĆ˝ĂćÖą˝Ç×řąęĎľxOyÖĐŁŹĂčłöÁËŇÔÉĎąíÖи÷śÔśÔӌ־Ϊ×řąęľÄľăŁŹ¸ůžÝĂčłöľÄľăŁŹťłö¸ĂşŻĘýľÄÍźĎóŁť
Ł¨4ŁŠ˝áşĎşŻĘýľÄÍźĎóŁŹÇëÍęłÉŁş
˘Ůľąy=Š![]() ĘąŁŹx=_____ŁŽ
ĘąŁŹx=_____ŁŽ
˘ÚĐ´łö¸ĂşŻĘýľÄŇťĚőĐÔÖĘ_____ŁŽ
˘ŰČôˇ˝łĚx+![]() =tÓĐÁ˝¸ö˛ťĎŕľČľÄĘľĘý¸ůŁŹÔňtľÄČĄÖľˇśÎ§ĘÇ_____ŁŽ
=tÓĐÁ˝¸ö˛ťĎŕľČľÄĘľĘý¸ůŁŹÔňtľÄČĄÖľˇśÎ§ĘÇ_____ŁŽ