题目内容
【题目】已知如图,抛物线y=ax2+bx+3与x轴交于点A(3,0),B(﹣1,0),与y轴交于点C,连接AC,点P是直线AC上方的抛物线上一动点(异于点A,C),过点P作PE⊥x轴,垂足为E,PE与AC相交于点D,连接AP.
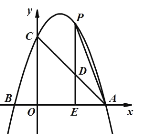
(1)求点C的坐标;
(2)求抛物线的解析式;
(3)①求直线AC的解析式;
②是否存在点P,使得△PAD的面积等于△DAE的面积,若存在,求出点P的坐标,若不存在,请说明理由.
【答案】(1)(0,3);(2)y=﹣x2+2x+3;(3)①![]() ;②当点P的坐标为(1,4)时,△PAD的面积等于△DAE的面积.
;②当点P的坐标为(1,4)时,△PAD的面积等于△DAE的面积.
【解析】
(1)将![]() 代入二次函数解析式即可得点C的坐标;
代入二次函数解析式即可得点C的坐标;
(2)把A(3,0),B(﹣1,0)代入y=ax2+bx+3即可得出抛物线的解析式;
(3)①设直线直线AC的解析式为![]() ,把A(3,0),C
,把A(3,0),C![]() 代入即可得直线AC的解析式;
代入即可得直线AC的解析式;
②存在点P,使得△PAD的面积等于△DAE的面积;设点P(x,﹣x2+2x+3)则点D(x,﹣x+3),可得PD=﹣x2+2x+3﹣(﹣x+3)=﹣x2+3x,DE=﹣x+3,根据S△PAD=S△DAE时,即可得PD=DE,即可得出结论.
解:(1)由y=ax2+bx+3,令![]()
∴点C的坐标为(0,3);
(2)把A(3,0),B(﹣1,0)代入y=ax2+bx+3得
![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为:y=﹣x2+2x+3;
(3)①设直线直线AC的解析式为![]() ,
,
把A(3,0),C![]() 代入得
代入得
![]() ,
,
解得![]() ,
,
∴直线AC的解析式为![]() ;
;
②存在点P,使得△PAD的面积等于△DAE的面积,理由如下:
设点P(x,﹣x2+2x+3)则点D(x,﹣x+3),
∴PD=﹣x2+2x+3﹣(﹣x+3)=﹣x2+3x,DE=﹣x+3,
当S△PAD=S△DAE时,有![]() ,得PD=DE,
,得PD=DE,
∴﹣x2+3x=﹣x+3解得x1=1,x2=3(舍去),
∴y=﹣x2+2x+3=﹣12+2+3=4,
∴当点P的坐标为(1,4)时,△PAD的面积等于△DAE的面积.

 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案【题目】“全民防控新冠病毒”期间某公司推出一款消毒产品,成本价8元/千克,经过市场调查,该产品的日销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)之间满足一次函数关系,该产品的日销售量与销售单价几组对应值如表:
(元/千克)之间满足一次函数关系,该产品的日销售量与销售单价几组对应值如表:
销售单价 | 12 | 16 | 20 | 24 |
日销售量 | 220 | 180 | 140 |
|
(注:日销售利润![]() 日销售量
日销售量![]() (销售单价
(销售单价![]() 成本单价)
成本单价)
(1)求![]() 关于
关于![]() 的函数解析式(不要求写出
的函数解析式(不要求写出![]() 的取值范围);
的取值范围);
(2)根据以上信息,填空:
①![]() _______千克;
_______千克;
②当销售价格![]() _______元时,日销售利润
_______元时,日销售利润![]() 最大,最大值是_______元;
最大,最大值是_______元;
(3)该公司决定从每天的销售利润中捐赠100元给“精准扶贫”对象,为了保证捐赠后每天的剩余利润不低于1500元,试确定该产品销售单价的范围.