ЬтФПФкШн
ЁОЬтФПЁПЃЈ1ЃЉШчЭМ1ЃЌНЋОиаЮABCDелЕўЃЌЪЙBCТфдкЖдНЧЯпBDЩЯЃЌелКлЮЊBEЃЌЕуCТфдкЕуCЁфДІЃЌШєЁЯADB=46ЁуЃЌдђЁЯDBEЕФЖШЪ§ЮЊЁЁ ЁЁЁуЃЎ
ЃЈ2ЃЉаЁУїЪжжагавЛеХОиаЮжНЦЌABCDЃЌAB=4ЃЌAD=9ЃЎ
ЃЈЛвЛЛЃЉ
ШчЭМ2ЃЌЕуEдкетеХОиаЮжНЦЌЕФБпADЩЯЃЌНЋжНЦЌелЕўЃЌЪЙABТфдкCEЫљдкжБЯпЩЯЃЌелКлЩшЮЊMNЃЈЕуMЃЌNЗжБ№дкБпADЃЌBCЩЯЃЉЃЌРћгУжБГпКЭдВЙцЛГіелКлMNЃЈВЛаДзїЗЈЃЌБЃСєзїЭМКлМЃЃЌВЂгУКкЩЋЫЎБЪАбЯпЖЮУшЧхГўЃЉЃЛ
ЃЈЫувЛЫуЃЉ
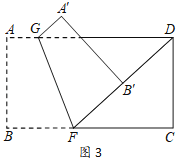
ШчЭМ3ЃЌЕуFдкетеХОиаЮжНЦЌЕФБпBCЩЯЃЌНЋжНЦЌелЕўЃЌЪЙFBТфдкЩфЯпFDЩЯЃЌелКлЮЊGFЃЌЕуAЃЌBЗжБ№ТфдкЕуAЁфЃЌBЁфДІЃЌШєAG=![]() ЃЌЧѓBЁфDЕФГЄЃЛ
ЃЌЧѓBЁфDЕФГЄЃЛ
ЃЈбщвЛбщЃЉ
ШчЭМ4ЃЌЕуKдкетеХОиаЮжНЦЌЕФБпADЩЯЃЌDK=3ЃЌНЋжНЦЌелЕўЃЌЪЙABТфдкCKЫљдкжБЯпЩЯЃЌелКлЮЊHIЃЌЕуAЃЌBЗжБ№ТфдкЕуAЁфЃЌBЁфДІЃЌаЁУїШЯЮЊBЁфIЫљдкжБЯпЧЁКУОЙ§ЕуDЃЌЫћЕФХаЖЯЪЧЗёе§ШЗЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉ23ЃЛЃЈ2ЃЉЁОЛвЛЛЁПЛЭММћНтЮіЃЛЁОЫувЛЫуЁПDBЁф =3ЃЛЁОбщвЛбщЁПаЁУїЕФХаЖЯВЛе§ШЗЃЌРэгЩМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнОиаЮаджЪПЩЕУADЁЮBCЃЌДгЖјПЩЕУЁЯADB=ЁЯDBC=46ЁуЃЌдйИљОнЗелЕФаджЪМДПЩЧѓЕУЁЯDBEЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЛвЛЛЃКСЌНгCEВЂбгГЄНЛBAЕФбгГЄЯпгыЕуGЃЌРћгУГпЙцзїЭМЛГіЁЯBGCЕФНЧЦНЗжЯпМДПЩЕУзЅКлMNЃЛ
ЫувЛЫуЃКгЩвбжЊПЩЕУGD=![]() ЃЌИљОнОиаЮЕФаджЪМАЗелЕФаджЪПЩЕУЁЯDFG=ЁЯDGFЃЌДгЖјПЩЕУDF=DG=
ЃЌИљОнОиаЮЕФаджЪМАЗелЕФаджЪПЩЕУЁЯDFG=ЁЯDGFЃЌДгЖјПЩЕУDF=DG=![]() ЃЌдкRtЁїCDFжаЃЌИљОнЙДЙЩЖЈРэПЩЧѓЕУCF=
ЃЌдкRtЁїCDFжаЃЌИљОнЙДЙЩЖЈРэПЩЧѓЕУCF=![]() ЃЌИљОнBF=BCЉCFЧѓЕУBFЕФГЄЃЌдйИљОнЗелЕФаджЪМЬЖјПЩЧѓЕУDBЁфЕФГЄМДПЩЃЛ
ЃЌИљОнBF=BCЉCFЧѓЕУBFЕФГЄЃЌдйИљОнЗелЕФаджЪМЬЖјПЩЧѓЕУDBЁфЕФГЄМДПЩЃЛ
бщвЛбщЃКШчЭМ4жаЃЌаЁУїЕФХаЖЯВЛе§ШЗЃЌСЌНгIDЃЌИљОнЙДЙЩЖЈРэЧѓГіCKГЄЃЌИљОнвбжЊПЩжЄУїЁїCDKЁзЁїIBЁфCЃЌДгЖјПЩЕУ![]() ЃЌЩшCBЁф=3kЃЌIBЁф=4kЃЌIC=5kЃЌИљОнелЕўЕФаджЪПЩЧѓЕУk=1ЃЌМЬЖјПЩЕУIC=5ЃЌIBЁф=4ЃЌBЁфC=3ЃЌдкRtЁїICBЁфжаЃЌtanЁЯBЁфIC=
ЃЌЩшCBЁф=3kЃЌIBЁф=4kЃЌIC=5kЃЌИљОнелЕўЕФаджЪПЩЧѓЕУk=1ЃЌМЬЖјПЩЕУIC=5ЃЌIBЁф=4ЃЌBЁфC=3ЃЌдкRtЁїICBЁфжаЃЌtanЁЯBЁфIC=![]() ЃЌСЌНгIDЃЌдкRtЁїICDжаЃЌtanЁЯDIC=
ЃЌСЌНгIDЃЌдкRtЁїICDжаЃЌtanЁЯDIC=![]() ЃЌДгЖјжЊtanЁЯBЁфICЁйtanЁЯDICЃЌХаЖЯГіBЁфIЫљдкЕФжБЯпВЛОЙ§ЕуDМДПЩЕУ.
ЃЌДгЖјжЊtanЁЯBЁфICЁйtanЁЯDICЃЌХаЖЯГіBЁфIЫљдкЕФжБЯпВЛОЙ§ЕуDМДПЩЕУ.
ЃЈ1ЃЉШчЭМ1жаЃЌ

ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрADЁЮBCЃЌ
ЁрЁЯADB=ЁЯDBC=46ЁуЃЌ
гЩЗелВЛБфадПЩжЊЃЌЁЯDBE=ЁЯEBC=![]() ЁЯDBC=23ЁуЃЌ
ЁЯDBC=23ЁуЃЌ
ЙЪД№АИЮЊЃК23ЃЛ
ЃЈ2ЃЉЛвЛЛЃКШчЭМ2жаЃЌ
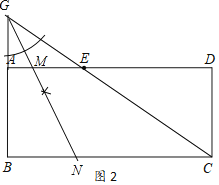
ЫувЛЫуЃКШчЭМ3жаЃЌ
ЁпAG=![]() ЃЌAD=9ЃЌ
ЃЌAD=9ЃЌ
ЁрGD=9Љ![]() =
=![]() ЃЌ
ЃЌ
ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрADЁЮBCЃЌ
ЁрЁЯDGF=ЁЯBFGЃЌ
гЩЗелВЛБфадПЩжЊЃЌЁЯBFG=ЁЯDFGЃЌ
ЁрЁЯDFG=ЁЯDGFЃЌ
ЁрDF=DG=![]() ЃЌ
ЃЌ
ЁпCD=AB=4ЃЌЁЯC=90ЁуЃЌ
ЁрдкRtЁїCDFжаЃЌCF=![]() =
=![]() ЃЌ
ЃЌ
ЁрBF=BCЉCF=![]() ЃЌ
ЃЌ
гЩЗелВЛБфадПЩжЊЃЌFB=FBЁф=![]() ЃЌ
ЃЌ
ЁрDBЁф=DFЉFBЁф=![]() Љ
Љ![]() =3ЃЛ
=3ЃЛ
бщвЛбщЃКШчЭМ4жаЃЌаЁУїЕФХаЖЯВЛе§ШЗЃЌ

РэгЩЃКСЌНгIDЃЌдкRtЁїCDKжаЃЌЁпDK=3ЃЌCD=4ЃЌ
ЁрCK=![]() =5ЃЌ
=5ЃЌ
ЁпADЁЮBCЃЌ
ЁрЁЯDKC=ЁЯICKЃЌ
гЩелЕўПЩжЊЃЌЁЯAЁфBЁфI=ЁЯB=90ЁуЃЌ
ЁрЁЯIBЁфC=90Ёу=ЁЯDЃЌ
ЁрЁїCDKЁзЁїIBЁфCЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
ЩшCBЁф=3kЃЌIBЁф=4kЃЌIC=5kЃЌ
гЩелЕўПЩжЊЃЌIB=IBЁф=4kЃЌ
ЁрBC=BI+IC=4k+5k=9ЃЌ
Ёрk=1ЃЌ
ЁрIC=5ЃЌIBЁф=4ЃЌBЁфC=3ЃЌ
дкRtЁїICBЁфжаЃЌtanЁЯBЁфIC=![]() ЃЌ
ЃЌ
СЌНгIDЃЌдкRtЁїICDжаЃЌtanЁЯDIC=![]() ЃЌ
ЃЌ
ЁрtanЁЯBЁфICЁйtanЁЯDICЃЌ
ЁрBЁфIЫљдкЕФжБЯпВЛОЙ§ЕуDЃЎ