题目内容
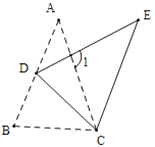
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() ,则
,则![]() ________.
________.
【答案】![]()
【解析】
过点A 作AF⊥BC于点,过点D 作DE⊥AC交AC的延长线于点E,目的得到直角三角形利用三角函数得△AFC三边的关系,再证明 △ACF∽△DCE,利用相似三角形性质得出△DCE各边比值,从而得解.
解:过点A 作AF⊥BC于点,过点D 作DE⊥AC交AC的延长线于点E,
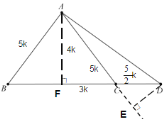
∵![]() ,
, ![]()
∴∠B=∠ACF,sin∠ACF=![]() =
=![]() ,
,![]()
设AF=4k,则AC=5k,CD=![]() ,由勾股定理得:FC=3k,
,由勾股定理得:FC=3k,
∵∠ACF=∠DCE,∠AFC=∠DEC=90°,
∴△ACF∽△DCE,
∴AC:CD=CF:CE=AF:DE,即5k: ![]() =3k:CE=4k:DE,
=3k:CE=4k:DE,
解得:CE=![]() ,DE=2k,即AE=AC+CE=5k+
,DE=2k,即AE=AC+CE=5k+![]() =
=![]() ,
,
∴在Rt△AED中,![]() DE:AE=2k:
DE:AE=2k:![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目