题目内容
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,﹣3),点P是直线BC下方抛物线上的任意一点。
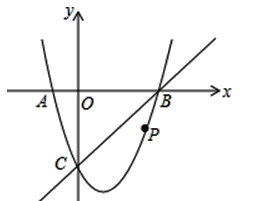
(1)求这个二次函数y=x2+bx+c的解析式。
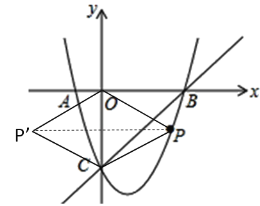
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形POP′C,如果四边形POP′C为菱形,求点P的坐标。
【答案】(1)二次函数的解析式为![]() ;(2)P(
;(2)P(![]() )时,四边形POP′C为菱形.
)时,四边形POP′C为菱形.
【解析】
(1)将点B、C的坐标代入解方程组即可得到函数解析式;
(2)根据四边形POP′C为菱形,得到![]() ,且
,且![]() 与OC互相垂直平分,可知点P的纵坐标为
与OC互相垂直平分,可知点P的纵坐标为![]() ,将点P的纵坐标代入解析式即可得到横坐标,由此得到答案.
,将点P的纵坐标代入解析式即可得到横坐标,由此得到答案.
(1)将点B(3,0)、C(0,﹣3)的坐标代入y=x2+bx+c,得
![]() ,∴
,∴![]()
∴二次函数的解析式为![]() ;
;
(2)如图,
令![]() 中x=0,得y=-3,
中x=0,得y=-3,
∴C(0,-3)
∵四边形POP′C为菱形,
∴![]() ,且
,且![]() 与OC互相垂直平分,
与OC互相垂直平分,
∴点P的纵坐标为![]() ,
,
当y=![]() 时,
时, ![]() ,
,
得: ![]() ,
,
∵点P是直线BC下方抛物线上的任意一点,
∴P(![]() )时,四边形POP′C为菱形.
)时,四边形POP′C为菱形.

练习册系列答案
相关题目