题目内容
【题目】定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到该边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1,△ABC中,点D是BC边上一点,连结AD,若![]() ,则称点D是△ABC中BC边上的“好点”.
,则称点D是△ABC中BC边上的“好点”.
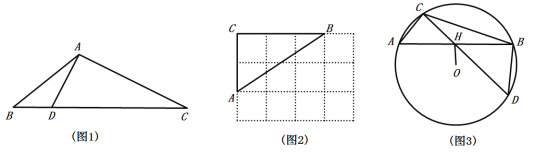
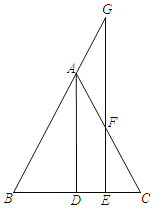
(1)如图2,△ABC的顶点是![]() 网格图的格点,请仅用直尺画出AB边上的一个“好点”.
网格图的格点,请仅用直尺画出AB边上的一个“好点”.
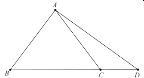
(2)△ABC中,BC=9,![]() ,
,![]() ,点D是BC边上的“好点”,求线段BD的长.
,点D是BC边上的“好点”,求线段BD的长.
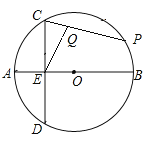
(3)如图3,△ABC是![]() 的内接三角形,OH⊥AB于点H,连结CH并延长交
的内接三角形,OH⊥AB于点H,连结CH并延长交![]() 于点D.
于点D.
①求证:点H是△BCD中CD边上的“好点”.
②若![]() 的半径为9,∠ABD=90°,OH=6,请直接写出
的半径为9,∠ABD=90°,OH=6,请直接写出![]() 的值.
的值.
【答案】(1)详见解析;(2)![]() 或5;(3)①详见解析;②
或5;(3)①详见解析;②![]() .
.
【解析】
(1)作AB边上的垂线或中线即可;
(2)作AE⊥BC于点E,根据三角函数求出BE、CE、AE的长,设DE为a,分①若点D在点E左侧②若点D在点E右侧,根据“好点”的定义进行求解即可;
(3)①根据“同弧或等弧所对的圆周角相等”证△AHC∽△DHB,再根据“好点”的定义判断即可;
②连接AD,根据∠ABD=90°判断AD为直径,用勾股定理求出AH的长,再根据勾股定理求出DH的长,根据①中的结论求出CH的长即可求得比值.
(1)如图所示:D点及为AB边上的“好点”
(2)作AE⊥BC于点E,由![]() ,
,![]() 可设AE=4x,
可设AE=4x,
则BE=3x,CE=6x,
∴BC=9x=9,∴![]() ,
,
∴BE=3,CE=6,AE=4,
设DE=a,
①若点D在点E左侧,
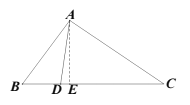
由点D是BC边上的“好点”知,![]() ,
,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
∴![]() .
.
②若点D在点E右侧,
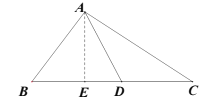
由点D是BC边上的“好点”知,![]() ,
,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,![]() (舍去)
(舍去)
∴![]() .
.
∴![]() 或5.
或5.
(3)①∵∠CHA=∠BHD,∠ACH=∠DBH
∴△AHC∽△DHB
∴![]() ,即
,即![]()
∵OH⊥AB
∴AH=BH
∴![]()
∴点H是△BCD中CD边上的“好点”.
②连接AD.
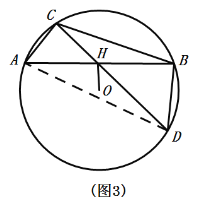
∵∠ABD=90°
∴AD为直径,
∵OH⊥AB,OH=6
∴![]() ,BD=2OH=12
,BD=2OH=12
∴BH=AH=![]()
∴![]()
由①得:![]()
即![]()
∴CH=![]()
∴![]() .
.