题目内容
【题目】在平面直角坐标系中,抛物线y=﹣![]() x+6与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
x+6与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
(1)如图1,点P为直线BC上方抛物线上一动点,过点P作PH∥y轴,交直线BC于点H,过点P作PQ⊥BC于点Q,当PQ﹣![]() PH最大时,点C关于x轴的对称点为点D,点M为直线BC上一动点,点N为y轴上一动点,连接PM、MN,求PM+MN+
PH最大时,点C关于x轴的对称点为点D,点M为直线BC上一动点,点N为y轴上一动点,连接PM、MN,求PM+MN+![]() ND的最小值;
ND的最小值;
(2)如图2,连接AC,将△OAC绕着点O顺时针旋转,记旋转过程中的△OAC为△OA'C',点A的对应点为点A',点C的对应点为点C'.当点A'刚好落在线段AC上时,将△OA'C'沿着直线BC平移,在平移过程中,直线OC'与抛物线对称轴交于点E,与x轴交于点F,设点R是平面内任意一点,是否存在点R,使得以B、E、F、R为顶点的四边形是菱形?若存在,请直接写出点R的坐标;若不存在,请说明理由.
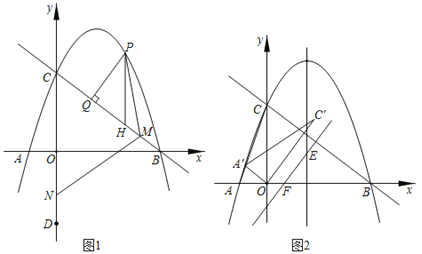
【答案】(1)![]() ;(2)存在,(
;(2)存在,(![]() ,10)或(
,10)或(![]() ,﹣
,﹣![]() )或(3,﹣
)或(3,﹣![]() )
)
【解析】
(1)PQ﹣![]() PH=PHsinα﹣PH=
PH=PHsinα﹣PH=![]() PH,当x=4时,PH最大,即PQ﹣
PH,当x=4时,PH最大,即PQ﹣![]() PH最大,此时点P(4,3);过点D作直线DH∥BC,则∠NDH=∠OBC,sin∠OCB=cos∠OBC=cosα=
PH最大,此时点P(4,3);过点D作直线DH∥BC,则∠NDH=∠OBC,sin∠OCB=cos∠OBC=cosα=![]() ,过点P作PH⊥DH于点H,则此时,PM+MN+
,过点P作PH⊥DH于点H,则此时,PM+MN+![]() ND的最小,即可求解;
ND的最小,即可求解;
(2)分BF是边、BF为对角线两种情况,分别求解即可.
解:(1)抛物线y=![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,
令x=0,则y=6;
令y=0,则![]() ,解得:
,解得:![]() ,
,![]() ;
;
∴点A、B、C的坐标分别为:(﹣2,0)、(8,0)、(0,6),
由点B、C的坐标得直线BC的表达式为:y=﹣![]() x+6,
x+6,
∴∠HPQ=∠OBC,则tan∠HPQ=tan∠OBC=![]() =tanα,
=tanα,
则sinα=![]() ,cos
,cos![]() ,
,
PQ﹣![]() PH=PHsinα﹣PH=
PH=PHsinα﹣PH=![]() PH,
PH,
而PH=y=![]() =
=![]() ,
,
当x=4时,PH最大,即PQ﹣![]() PH最大,
PH最大,
此时点P(4,3);
过点D作直线DH∥BC,则∠NDH=∠OBC,sin∠OCB=cos∠OBC=cosα=![]() ,
,
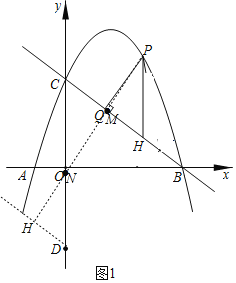
过点P作PH⊥DH于点H,则此时,PM+MN+![]() ND的最小,
ND的最小,
则HD=DNsin∠NDH=DNcosα=![]() ,
,
则PM+MN+![]() ND=PM+MN+HN=PH,即此时PM+MN+
ND=PM+MN+HN=PH,即此时PM+MN+![]() ND的最小,
ND的最小,
直线PH⊥HD,则直线PH表达式中的k值为:![]() ,
,
由k值和点P的坐标得:直线PH的表达式为:y=![]() x,故点N(0,0),
x,故点N(0,0),
HN=NDcosα=6×![]() =
=![]() ,PN=PO=5,
,PN=PO=5,
PH=5+![]() =
=![]() ,
,
即PM+MN+![]() ND的最小值为:
ND的最小值为:![]() ;
;
(2)OA=OA′=2,
过点A′作A′H⊥x轴于点H,tan∠A′AO=![]() =3=tanβ,
=3=tanβ,
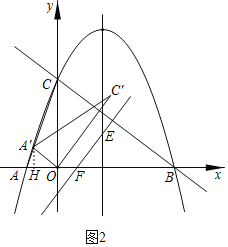
设AH=x,则A′H=3x,OH=2﹣x,
由勾股定理得:22=(3x)2+(2﹣x)2,
解得:x=![]() ,故点A′(﹣
,故点A′(﹣![]() ,
,![]() ),
),
则直线OA′的表达式为:y=﹣![]() x,
x,
OA′⊥C′O,则直线OC′的表达式为:y=![]() x,
x,
设直线OC′向右平移了m个单位,则直线OC′的表达式为:y=![]() (x﹣m),
(x﹣m),
抛物线的对称轴为:x=3,
则点F(m,0),点E(3,4﹣![]() m),而点B(8,0);
m),而点B(8,0);
①当BF是边时,
则BF=ER=8﹣m,则点R(3+8﹣m,4﹣![]() m),
m),
由BR=FR得:(8﹣m)2=(3﹣m)2+(4﹣![]() m)2,
m)2,
解得:m=﹣![]() 或
或![]() ,
,
故点R(![]() ,10)或(
,10)或(![]() ,﹣
,﹣![]() );
);
②当BF为对角线时,
则点R(3,![]() m﹣4),
m﹣4),
由FR=BR得:(m﹣3)2+(![]() m﹣4)2=52+(
m﹣4)2=52+(![]() m﹣4)2,
m﹣4)2,
解得:m=8(舍去)或﹣2,
故点R(3,﹣![]() );
);
综上所述,点R的坐标为:(![]() ,10)或(
,10)或(![]() ,﹣
,﹣![]() )或(3,﹣
)或(3,﹣![]() ).
).