题目内容

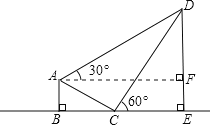
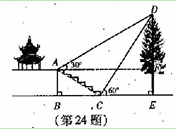
【题目】(本题7分)如图，某校综合实践活动小组的同学欲测量公园内一棵树DE的高度．他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°．已知A点的高度AB为2米，台阶AC的坡度为 (即AB：BC=)，且B、C、E三点在同一条盲线上。请根据以上杀件求出树DE的高度(测倾器的高度忽略不计)．

【答案】解：树DE的高度为6米。

【解析】

如图，过点A作AF⊥DE于F，

则四边形ABEF为矩形，

∴AF=BE，EF=AB=2，

设DE=x，

在Rt△CDE中，CE==x，

在Rt△ABC中，

∵=，AB=2，

∴BC=2，

在Rt△AFD中，DF=DE﹣EF=x﹣2，

∴AF==（x﹣2），

∵AF=BE=BC+CE，

∴（x﹣2）=2+x，

解得x=6．

答：树高为6米．

练习册系列答案
相关题目

【题目】为了了解初中阶段女生身高情况，从某中学初二年级120名女生中随意抽出40名同龄女生的身高数据，经过分组整理后的频数分布表及频数分布直方图如图所示：

结合以上信息，回答问题：

（1）a=______，b=______，c=______．

（2）请你补全频数分布直方图．

（3）试估计该年级女同学中身高在160～165cm的同学约有多少人？

【题目】如图，AB是⊙O的直径，PB与⊙O相切于点B，连接PA交⊙O于点C，连接BC．

（1）求证：∠BAC=∠CBP；

（2）求证：PB2=PCPA；

（3）当AC=6，CP=3时，求sin∠PAB的值．

【题目】如图，已知抛物线的顶点为A（1，4），抛物线与y轴交于点B（0，3），与x轴交于C，D两点．点P是x轴上的一个动点．

（1）求此抛物线的解析式；

（2）当PA+PB的值最小时，求点P的坐标；

（3）抛物线上是否存在一点Q（Q与B不重合），使△CDQ的面积等于△BCD的面积？若存在，直接写出点Q的坐标；若不存在，请说明理由．

【题目】如图，在平面直角坐标系中，直线l：y=x﹣与x轴交于点B1，以OB1为边长作等边三角形A1OB1，过点A1作A1B2平行于x轴，交直线l于点B2，以A1B2为边长作等边三角形A2A1B2，过点A2作A2B3平行于x轴，交直线l于点B3，以A2B3为边长作等边三角形A3A2B3，…，则点A2017的横坐标是 ．

【题目】在直角坐标系中，过原点O及点A（8，0），C（0，6）作矩形OABC、连结OB，点D为OB的中点，点E是线段AB上的动点，连结DE，作DF⊥DE，交OA于点F，连结EF．已知点E从A点出发，以每秒1个单位长度的速度在线段AB上移动，设移动时间为t秒．

（1）如图1，当t=3时，求DF的长．

（2）如图2，当点E在线段AB上移动的过程中，∠DEF的大小是否发生变化？如果变化，请说明理由；如果不变，请求出tan∠DEF的值．

（3）连结AD，当AD将△DEF分成的两部分的面积之比为1：2时，求相应的t的值．

【题目】如图，已知⊙O 的直径 AB 垂直弦 CD 于点 E，连接 CO 并延长交 AD于点 F，且 CF⊥AD

（1）求证：点 E 是 OB 的中点；

（2）若 AB=12，求 CD 的长．

【题目】如图，在等边中，是边上一点，连接，将绕点逆时针旋转得到，连接，若，，则有以下四个结论：①是等边三角形；②；③的周长是10；④．其中正确结论的序号是（ ）

A.②③④B.①③④C.①②④D.①②③

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网