题目内容
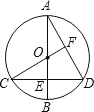
【题目】如图,已知⊙O 的直径 AB 垂直弦 CD 于点 E,连接 CO 并延长交 AD于点 F,且 CF⊥AD
(1)求证:点 E 是 OB 的中点;
(2)若 AB=12,求 CD 的长.
【答案】(1)证明见解析(2)6![]()
【解析】
(1)如图,连接AC.想办法证明△ACD是等边三角形,推出∠OCE=30°即可解决问题;
(2)根据垂径定理CD=2EC,求出EC即可解决问题;
(1)证明:如图,连接 AC.
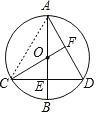
∵AB⊥CD 于点 E,
∴CE=DE,
在△ACE 和△ADE 中,
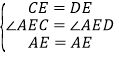 ,
,
∴△ACE≌△ADE(SAS),
∴AC=AD,
同理:CA=CD,
∴△ACD 是等边三角形,
∴∠OCE=30°,
∴OE= ![]() OC
OC
而 OB=OC,
∴OE= ![]() OB.
OB.
故 E 是 OB 的中点.
(2)解:∵AB=12,
∴OC=6,
∴OE= ![]() OC=3,
OC=3,
在 Rt△OCE 中,
CE=![]() =
=![]() =3
=3![]() ,
,
∴CD=2CE=6![]() .
.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目