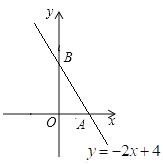题目内容
【题目】已知y+2与x成正比例,且x=-2时,y=0
(1)求y与x之间的函数表达式,并画出函数的图象;
(2)利用图象直接写出:当y>0时,x的取值范围;
(3)设点P在y轴负半轴上,(2)中的图象与x轴,y轴分别交于A,B两点,且S△ABP=4,求P点的坐标
【答案】(1)y=-x-2,见解析;(2)x<-2;(3)(0,-6)
【解析】
(1)根据两个式子成正比例,设出关系式,将点的坐标代入即可得到函数的表达式,并画图;
(2)根据图象得到y与x轴的交点,而交点左边的x的取值范围即为y>0时,x的取值范围;
(3)根据题意计算得到点A以及点B的坐标,根据三角形的面积公式列出式子即可得到点P的坐标.
(1)解:设y+2=kx,
当x=-2时,y=0
有0+2=-2k,
解得k=-1,
故y与x之间的函数关系式是y=-x-2;
如图:
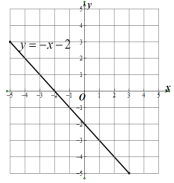
(2)解:当![]() 时,
时,![]()
由图可得:当y>0时,x<-2
(3)解:由(1)可得A的坐标(-2,0),B的坐标(0,-2),
根据题意可得:S△ABP= ![]() ×|-2|×BP=4,
×|-2|×BP=4,
解得BP=4,故点P的坐标为(0,-6)或(0,2),
又点P在y轴负半轴上,故点P的坐标为(0,-6).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目