题目内容
【题目】(1)模型建立:
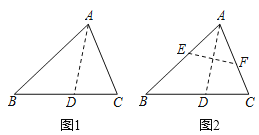
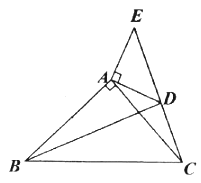
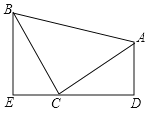
如图,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,过
,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() .求证:
.求证:![]() ;
;
(2)模型应用:
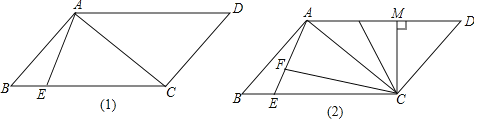
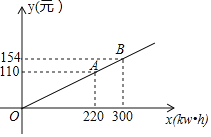
①如图,一次函数![]() 的图象分别与
的图象分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,以线段
,以线段![]() 为腰在第一象限内作等腰直角三角形
为腰在第一象限内作等腰直角三角形![]() ,则
,则![]() 点的坐标为___________(直接写出结果)
点的坐标为___________(直接写出结果)
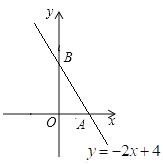
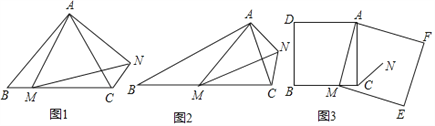
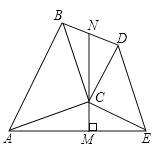
②如图,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,连接
,连接![]() 、
、![]() ,作
,作![]() 于
于![]() 点,延长
点,延长![]() 与
与![]() 交于点
交于点![]() ,求证:
,求证:![]() 是
是![]() 的中点.
的中点.
【答案】(1)见解析;(2)①![]() 或
或![]() ,②见解析
,②见解析
【解析】
(1)利用同角的余角相等判断出∠CAD=∠BCE,然后利用AAS证明全等,即可得出结论;
(2)①先求出点A和点B的坐标,得到BO=4,AO=2,由![]() 为等腰直角三角形,可分为两种情况:AB=AC或AB=BC,分别求出点C坐标即可;
为等腰直角三角形,可分为两种情况:AB=AC或AB=BC,分别求出点C坐标即可;
②作![]() 交
交![]() 的延长线于
的延长线于![]() ,作
,作![]() 于
于![]() ,先由AAS证明
,先由AAS证明![]() ≌
≌![]() ,得到
,得到![]() ,同理可证
,同理可证![]() ,则
,则![]() ,然后证明
,然后证明![]() ≌
≌![]() ,即可得到结论.
,即可得到结论.
解:(1)![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中
中
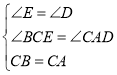 ,
,
![]() ;
;
(2)①∵一次函数![]() 的图象分别与
的图象分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,
,
令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() ;
;
∴点A为(2,0),点B为(0,4),
∴BO=4,AO=2;
∵![]() 为等腰直角三角形,
为等腰直角三角形,
当AB=AC时,有∠BAC=90°,如图:
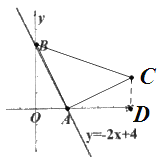
与(1)同理,得△ABO≌△CAD,
∴AD=BO=4,CD=AO=2,
∴OD=AO+AD=2+4=6,
∴点C的坐标为:![]() ;
;
当AB=BC时,有∠ABC=90°,如图:
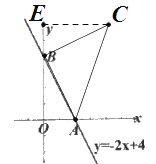
与(1)同理,得△ABO≌△BCE,
∴CE=BO=4,BE=AO=2,
∴OE=2+4=6,
∴点C坐标为:![]() ;
;
故答案为:![]() 或
或![]() .
.
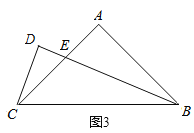
②如图,作![]() 交
交![]() 的延长线于
的延长线于![]() ,作
,作![]() 于
于![]() ,
,
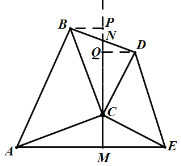
![]() ,
,
![]() ,
,
![]() ;
;
在![]() 与
与![]() 中,
中,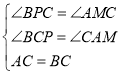 ,
,
![]() ,
,
![]() ,
,
同理,![]() ,
,
![]() ,
,
在![]() 与
与![]() 中,
中,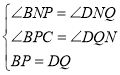 ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的中点.
的中点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目