题目内容
【题目】抛物线y=x2﹣2x﹣3与交y轴负半轴于C点,直线y=kx+2交抛物线于E、F两点(E点在F点左边).使△CEF被y轴分成的两部分面积差为5,则k的值为_____.
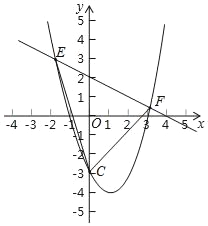
【答案】﹣4
【解析】
设直线y=kx+2交抛物线于E、F两点的横坐标分别为x1,x2,且(x1<0,x2>0),根据题意得出x1+x2=2+k,然后根据△CEF被y轴分成的两部分面积差为5,列出关于k的方程,解方程即可.
设直线y=kx+2交抛物线于E、F两点的横坐标分别为x1,x2,且(x1<0,x2>0),
由题意可知:x1,x2是方程x2-2x-3=kx+2的两个根,
整理方程为:x2-(2+k)x-5=0,
∴x1+x2=2+k,
由抛物线y=x2-2x-3可知C(0,-3),
设直线y=kx+2交y轴于B,
∴B(0,2),
∴BC=5,
∵△CEF被y轴分成的两部分面积差为5,
∴|S△BCE-S△BCF|=5,
当S△BCE-S△BCF=5时,则有![]() ×5x2-
×5x2-![]() ×5(-x1)=5,
×5(-x1)=5,
整理得:
![]() (x1+x2)=5,
(x1+x2)=5,
∴![]() (2+k)=5,解得k=0(舍去),
(2+k)=5,解得k=0(舍去),
当S△BCE-S△BCF=-5时,则有![]() ×5x2-
×5x2-![]() ×5(-x1)=-5,
×5(-x1)=-5,
整理得:![]() (x1+x2)=-5,
(x1+x2)=-5,
∴![]() (2+k)=-5,解得k=-4,
(2+k)=-5,解得k=-4,
故答案是:-4.

练习册系列答案
相关题目