题目内容
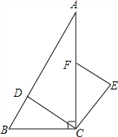
【题目】如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△AED;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF.其中正确的是_____.

【答案】①②⑤
【解析】
由平行四边形的性质得出AD∥BC,AD=BC,由AE平分∠BAD,可得∠BAE=∠DAE,可得∠BAE=∠BEA,得AB=BE,由AB=AE,得到△ABE是等边三角形,②正确;则∠ABE=∠EAD=60°,由SAS证明△ABC≌△EAD,①正确;由△FCD与△ABD等底(AB=CD)等高(AB与CD间的距离相等),得出S△FCD=S△ABD,由△AEC与△DEC同底等高,所以S△AEC=S△DEC,得出S△ABE=S△CEF.⑤正确.
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠EAD=∠AEB,
又∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE,
∵AB=AE,
∴△ABE是等边三角形;
②正确;
∴∠ABE=∠EAD=60°,
∵AB=AE,BC=AD,
∴△ABC≌△EAD(SAS);
①正确;
∵△FCD与△ABC等底(AB=CD)等高(AB与CD间的距离相等),
∴S△FCD=S△ABC,
又∵△AEC与△DEC同底等高,
∴S△AEC=S△DEC,
∴S△ABE=S△CEF;
⑤正确.
若AD与AF相等,即∠AFD=∠ADF=∠DEC,
即EC=CD=BE,
即BC=2CD,
题中未限定这一条件,
∴③④不一定正确;
故答案为:①②⑤.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案【题目】现有两个可以自由转动的转盘,每个转盘分成三个相同的扇形,涂色情况如图所示,指针的位置固定,同时转动两个转盘,回答以下问题:

圆1 圆2
圆2 圆1 | |||
(1)补全表格:圆1的所有可能结果有 种,分别是 ;
圆2的所有可能结果有 种,分别是 .
(2)写出:转盘停止后指针指向同种颜色区域的概率和至少有一指针指向红色区域的概率.