题目内容
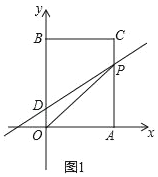
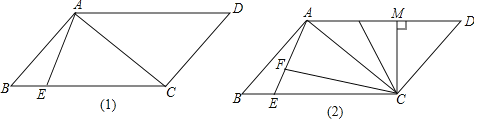
【题目】如图1,直线![]() 与直线
与直线![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() ,
,![]() 与
与![]() 互补.
互补.
(1)试判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
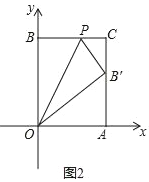
(2)如图2,![]() 与
与![]() 的角平分线交于点
的角平分线交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 是
是![]() 上一点,且
上一点,且![]() ,求证:
,求证:![]() .
.
(3)如图3,在(2)的条件下,连接![]() ,
,![]() 是
是![]() 上一点使
上一点使![]() ,作
,作![]() 平分
平分![]() ,求
,求![]() 的度数.
的度数.



【答案】(1)AB//CD,理由见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)利用对顶角相等、等量代换可以推知同旁内角∠AEF、∠CFE互补,即可证明;
(2)利用(1)中平行线的性质、角平分线的性质、三角形内角和定理可得∠EPF=90°,即EG⊥PF,再结合GH⊥EG,即可证明;
(3)利用三角形外角定理、三角形内角和定理求得∠A=90°-∠3=90°-2∠2;然后由邻补角的定义、角平分线的定义推知∠QPK=-![]() ∠EPK=45°+∠2,最后根据角与角间的和差关系即可求解.
∠EPK=45°+∠2,最后根据角与角间的和差关系即可求解.
(1)![]() ,
,
理由如下:如图1,
图1
∵![]() 与
与![]() 互补,
互补,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)如图2,由(1)知,![]() ,
,
图2 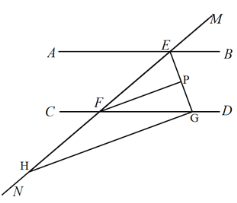
∴![]() .
.
又∵![]() 与
与![]() 的角平分线交于点
的角平分线交于点![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() .
.
∵![]() ,
,
∴![]() ;
;
(3)如图3,
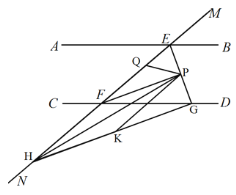
∵![]() ,
,
![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() 平分
平分![]() ,
,
∴![]() .
.
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目