题目内容
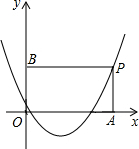
已知在平面直角坐标系xOy中，二次函数y=x2-bx+c（b＞0）的图象经过点A（-1，b），与y轴相交于点B，且∠ABO的余切值为3．
（1）求点B的坐标；
（2）求这个函数的解析式；
（3）如果这个函数图象的顶点为C，求证：∠ACB=∠ABO．
（1）求点B的坐标；
（2）求这个函数的解析式；
（3）如果这个函数图象的顶点为C，求证：∠ACB=∠ABO．
（1）根据题意，得b=1+b+c．
∴c=-1．
∴B（0，-1）；
（2）过点A作AH⊥y轴，垂足为点H．
∵∠ABO的余切值为3，∴cot∠ABO=
=3．
而AH=1，∴BH=3．
∵BO=1，∴HO=2．
∴b=2．
∴所求函数的解析式为y=x2-2x-1；
（3）由y=x2-2x-1=（x-1）2-2，得顶点C的坐标为（1，-2）．
∴AC=2
，AB=
，BC=
，AO=
，BO=1．
∴
=
=
=
．
∴△ABC∽△AOB．
∴∠ACB=∠ABO．
∴c=-1．
∴B（0，-1）；
（2）过点A作AH⊥y轴，垂足为点H．
∵∠ABO的余切值为3，∴cot∠ABO=
| BH |
| AH |
而AH=1，∴BH=3．
∵BO=1，∴HO=2．
∴b=2．
∴所求函数的解析式为y=x2-2x-1；
（3）由y=x2-2x-1=（x-1）2-2，得顶点C的坐标为（1，-2）．
∴AC=2
| 5 |
| 10 |
| 2 |
| 5 |
∴
| AC |
| AB |
| AB |
| AO |
| BC |
| BO |
| 2 |
∴△ABC∽△AOB．
∴∠ACB=∠ABO．
练习册系列答案
相关题目
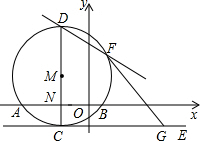直于x轴于N，直线CE切圆M于C，直线FG切圆M于F，交CE于G，已知点G的横坐标为3，
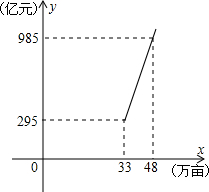用地总量x（万亩）之间存在着如图所示的一次函数关系．
