��Ŀ����
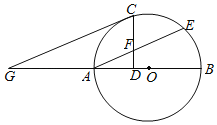
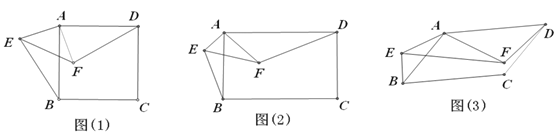
����Ŀ����ͼ��ʾ����1��������ABCD������Rt��AEF�й�������A,��EAF��90��, ����BE��DF.��Rt��AEF�Ƶ�A��ת,����ת�����У�BE��DF����������������ϵ��λ�ù�ϵ�����ͼ(1)����֤����
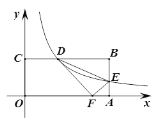
(2)����1���е�������ABCD��Ϊ����ABCD������Rt��AEF��ΪRt��AEF����AD��kAB,AF��kAE,������������.(1)�еĽ����Ƿ����仯�����ͼ(2)˵�����ɣ�
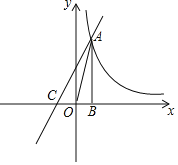
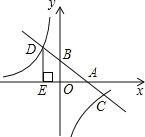
(3)����2���еľ���ABCD��Ϊƽ���ı���ABCD����Rt��AEF��Ϊ��AEF���ҡ�BAD����EAF��![]() ��������������.(2)�еĽ����Ƿ����仯�����ͼ(3)��������䣬ֱ��д�����ۣ�����仯��ֱ����k��ʾ���߶�BE��DF��������ϵ����
��������������.(2)�еĽ����Ƿ����仯�����ͼ(3)��������䣬ֱ��д�����ۣ�����仯��ֱ����k��ʾ���߶�BE��DF��������ϵ����![]() ��ʾ��ֱ��BE��DF�γɵ����
��ʾ��ֱ��BE��DF�γɵ����![]() .
.
���𰸡���1��DF=BE��DF��BE��֤������������2��������ϵ�ı䣬λ�ù�ϵ���䣬��DF=kBE��DF��BE����3�����ı䣮DF=kBE����=180��-��
�������������������1��������ת�Ĺ������߶εij��Ȳ��䣬�õ�AF=AE������BAE����DAF������BAF���࣬������BA E=��DAF��������FAD�ա�EAB�����BE��DF��ȣ��ӳ�DF��BE��G������ȫ�������εĶ�Ӧ����Ⱥ��ı��ε��ڽǺ͵���360�������EGF=90��������DF��BE����2����ͬ��1���ķ�������Ϊ���ε��ڱ߲���ȣ����������⣬���Եõ���Ӧ�߳ɱ�����������FAD�ס�EAB������DF=kBE��ͬ�����������������εĶ�Ӧ����Ⱥ��ı��ε��ڽǺ͵���360�������EHF=90��������DF��BE��
��3���루2����֤��������ͬ�����������������εĶ�Ӧ����Ⱥ��ı��ε��ڽǺ͵���360�������EAF+��EHF=180��������DF��BE�ļн���=180��-����
�����������1��DF��BE���ഹֱ����ȣ�
֤�����ӳ�DF�ֱ�AB��BE�ڵ�P��G
��������ABCD�͵���ֱ����AEF��
AD=AB��AF=AE��
��BAD=��EAF=90��
���FAD=��EAB
���FAD�ա�EAB��2�֣�
���AFD=��AEB��DF="BE"
�ߡ�AFD+��AFG=180����
���AEG+��AFG=180����
�ߡ�EAF=90����
��DF��BE
��2��������ϵ�ı䣬λ�ù�ϵ���䣮DF=kBE��DF��BE��
�ӳ�DF��EB�ڵ�H��
��AD=kAB��AF="kAE"
��![]() ,
, ![]()
��![]()
�ߡ�BAD=��EAF="a"
���FAD=��EAB
���FAD�ס�EAB
��![]()
��DF="kBE"
�ߡ�FAD�ס�EAB��
���AFD=��AEB��
�ߡ�AFD+��AFH=180����
���AEH+��AFH=180����
�ߡ�EAF=90����
���EHF=180��-90��=90����
��DF��BE


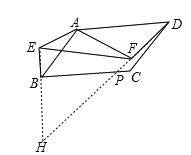
��3�����ı䣮DF=kBE����=180��-a��
�ӳ�DF��EB���ӳ����ڵ�H��
��AD=kAB��AF="kAE"
��![]() ,
, ![]()
��![]()
�ߡ�BAD=��EAF="a"
���FAD=��EAB
���FAD�ס�EAB
��![]()
��DF=kBE
����FAD�ס�EAB����AFD=��AEB
�ߡ�AFD+��AFH=180��
���AEB+��AFH=180��
���ı���AEHF���ڽǺ�Ϊ360����
���EAF+��EHF=180��
�ߡ�EAF=������EHF=��
��a+��=180����=180��-a

 �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д� ��������ϵ�д�
��������ϵ�д� ���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�