题目内容
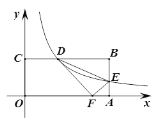
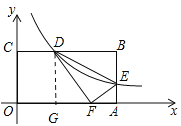
【题目】如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B 的坐标为(8,4),反比例函数y=![]() (k>0)的图象分别交边BC、AB 于点D、E,连结DE,△DEF与△DEB关于直线DE对称,当点F恰好落在线段OA上时,则k的值是________.
(k>0)的图象分别交边BC、AB 于点D、E,连结DE,△DEF与△DEB关于直线DE对称,当点F恰好落在线段OA上时,则k的值是________.
【答案】12
【解析】
由于四边形是矩形OABC,且△DEF与△DEB关于直线DE对称.当点F正好落在边OA上,可得△DGF∽△FAE,然后把D和E点坐标表示出来,再由三角形相似对应边成比例即可求出AF的长.然后利用勾股定理求出k=12.
过点D作DG⊥OA垂足为G(如图所示)
由题意知D(![]() ,4),E(8,
,4),E(8,![]() ),DG=4
),DG=4
又∵△DEF与△DEB关于直线DE对称.当点F正好落在边OA上
∴DF=DB,∠B=∠DFE=90°
∵∠DGF=∠FAE=90°,∠DFG+∠EFA=90°
又∵∠EFA+∠FEA=90°
∴∠GDF=∠EFA
∴△DGF∽△FAE
∴![]() ,即
,即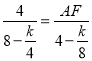 ,
,
解得:AF=2,
∵EF2=EA2+AF2
即(4![]() )2=(
)2=(![]() )2+4
)2+4
解得:k=12
故答案为12

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
【题目】为了提高学生的身体素质,某班级决定开展球类活动,要求每个学生必须在篮球、足球、排球、乒乓球、羽毛球中选择一项参加训练(只选择一项),根据学生的报名情况制成如下统计表:
项目 | 篮球 | 足球 | 排球 | 乒乓球 | 羽毛球 |
报名人数 | 12 | 8 | 4 | a | 10 |
占总人数的百分比 | 24% | b |
(1)该班学生的总人数为 人;
(2)由表中的数据可知:a= ,b= ;
(3)报名参加排球训练的四个人为两男(分别记为A、B)两女(分别记为C、D),现要随机在这4人中选2人参加学校组织的校级训练,请用列表或树状图的方法求出刚好选中一男一女的概率.